Intro do Datových Struktur

Datové struktury jsou něco, co používáme při programování pořád. Často ale ani nepřemýšlíme nad tím, jak dané datové struktury fungují. V tomto článku vás provedu několika nejpoužívanějšími datovými strukturami, jejich výhodami, a tím, jak je napsat v jazyce C.

Základní Termíny

Před tím, než začneme s datovými strukturami samotnými projdu krátce nějáké základní termíny. Pokud se cítíte, že těmto termínům rozumíte nebojte se tuto sekci přeskočit.

Stack

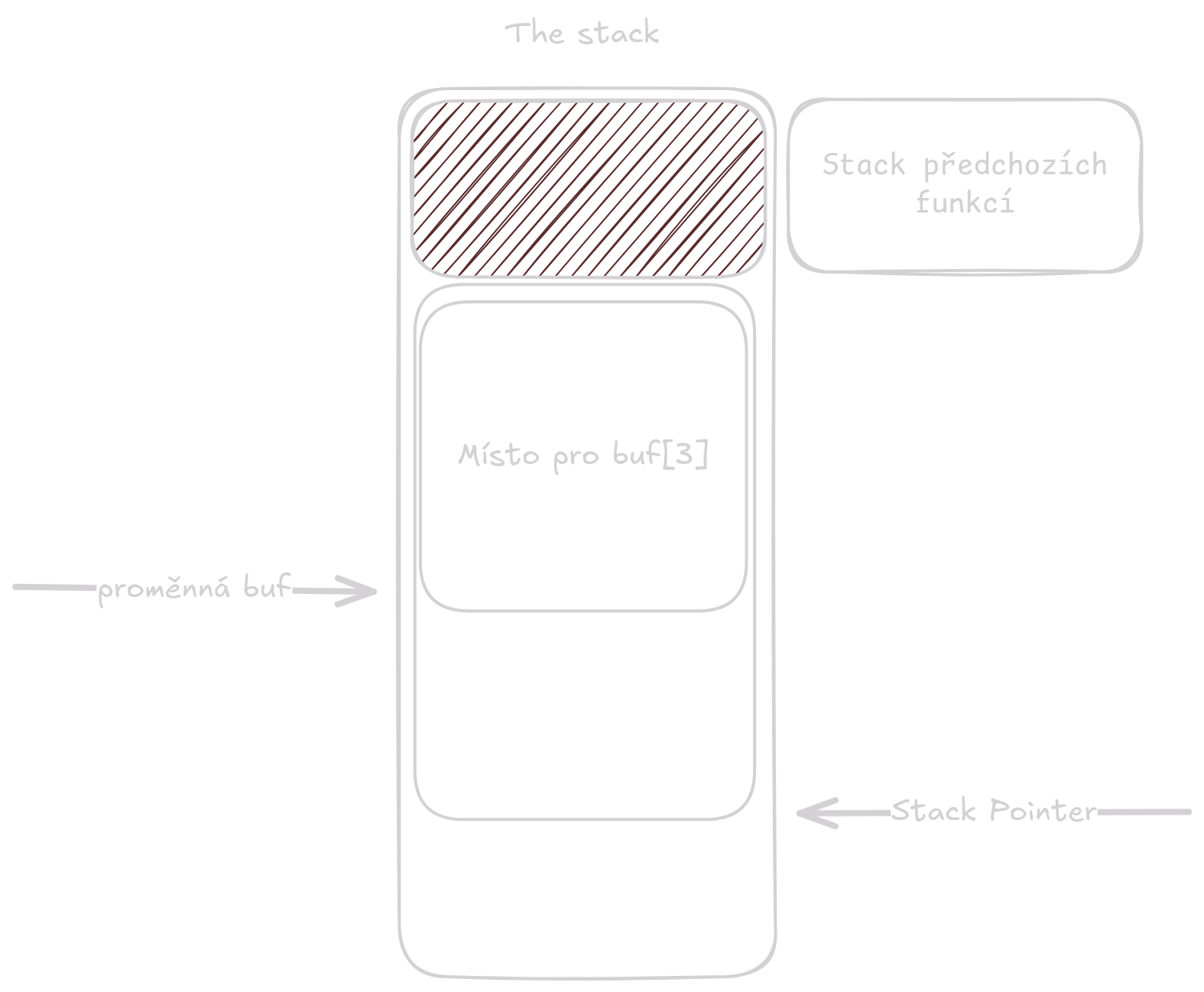
Stack je místo v paměti kde jsou na sebe naskládaná data pro funkce. Dávají se sem proměnné, které mají známou velikost při kompilaci. V následujícím příkladě bude proměnná buf[3] žít na stacku.

#include <stdio.h>
#include <unistd.h>

int main() {
  char buf[3];
  fgets(buf, 3, STDIN_FILENO);
  return 0;
}

Pro více info se koukněte na předchozí článek na sekci stack

Heap

Na heap dáváme data, u kterých nevíme jejich velikost předem nebo data, která potřebujeme, aby žily napříč více funkcemi (promněnné na stacku funkce zmizí poté co funkce skončí). Heap se nachází ve virtual address space našeho programu stejně jako stack a vypadá asi nějak takto:

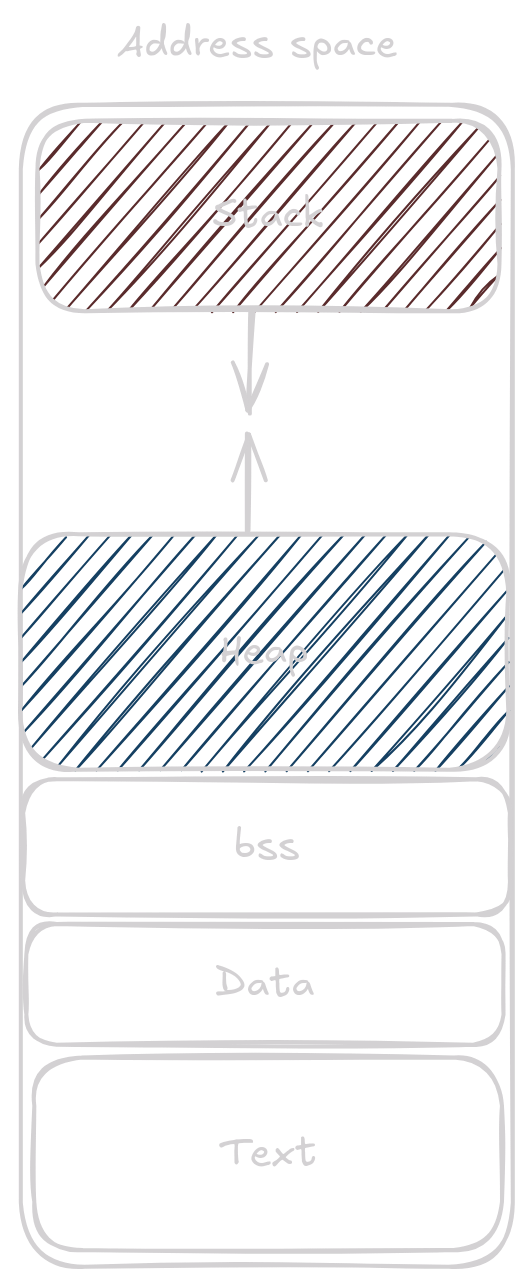
Často je si ale jednodušší představit stack jako místo kde jsou proměnné na sebe těsně naskládané a žijou jen po dobu běhu jednotlivé funkce a heap jako místo kde je spousta prostoru a data tam jsou, dokud se nerozhodneme je uklidit.

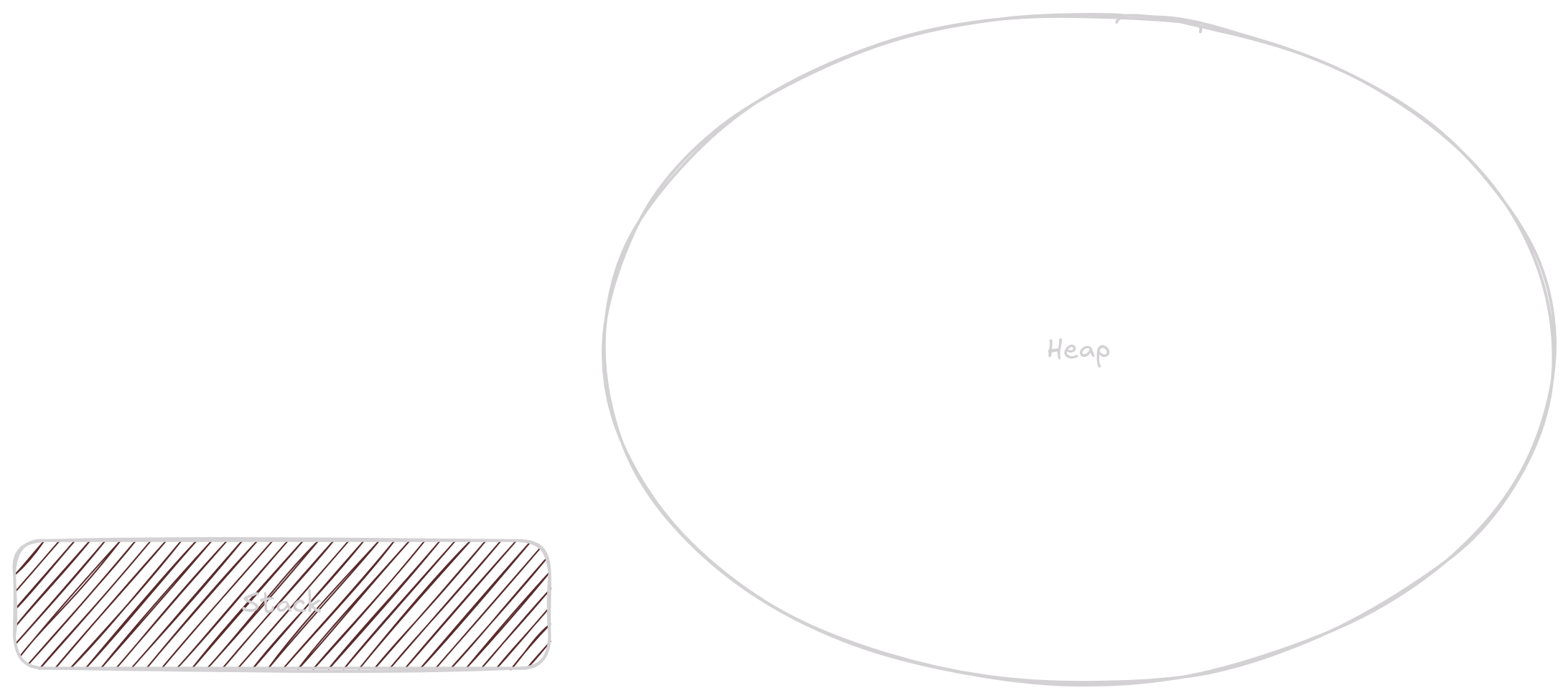
Pointery

Pointer se překládá jako ukazatel což tak nějak přesně popisuje, co pointer je. Pointer ukazuje někam do paměti, kde jsou jiná data, co nás zajímají. Důležité je vědět, že i když nevíme. jak velká jsou data, na které pointer ukazuje velikost pointeru samotného je vždy známá. V příkladě výše jsme použily pointer abychom funkci fgets() předali informaci kam má uložit přečtená data.

#include <stdio.h>
#include <unistd.h>

int main() {
  char buf[3];
  fgets(buf, 3, STDIN_FILENO);
  return 0;
}

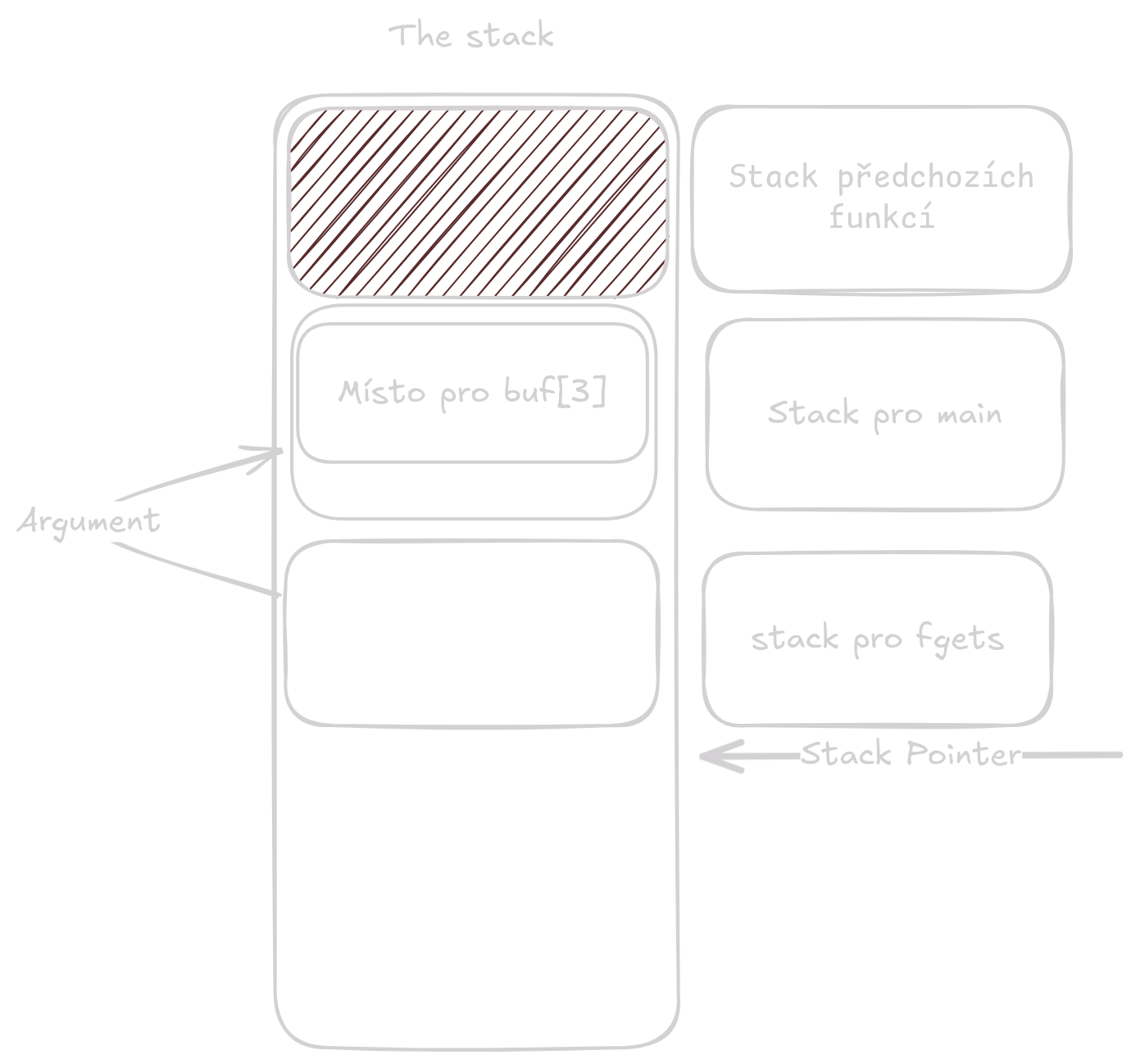
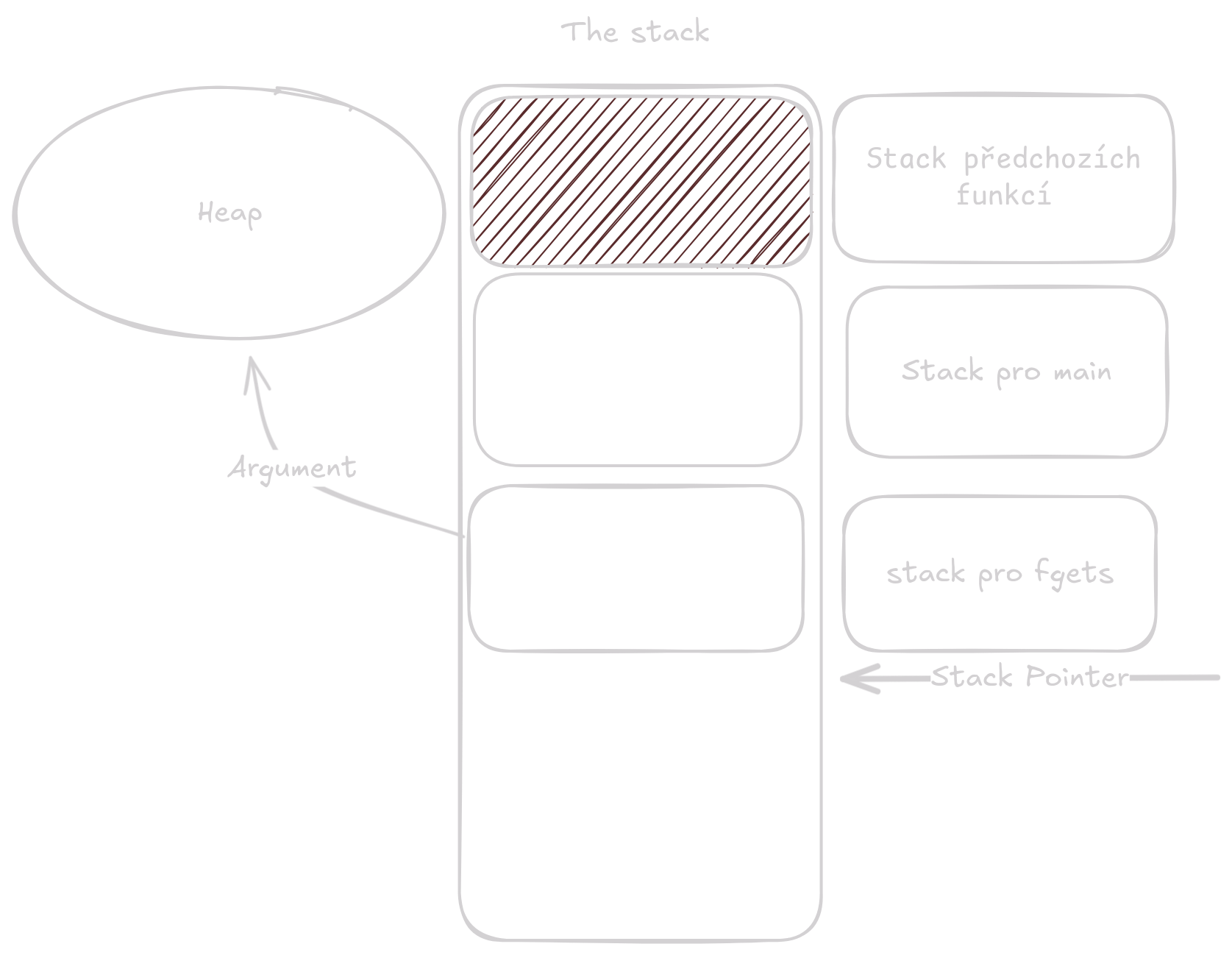
Funkce má jako argument pointer, který ukazuje někam do paměti to kam pointer ukazuje je funkci úplně jedno.

V tomto příkladě pointer ukazuje na heap kde je někde naše alokovaná paměť.

int main() {
  char *buf = malloc(sizeof(char) * 3);
  fgets(buf, 3, STDIN_FILENO);
  return 0;
}

Pointer na proměnnou můžeme získat pomocí znaménka &.

void foo(int c, int *d, int *e) {
  // změní hodnotu proměnné c ale nic to neudělá s argumentem a daný do funkce foo
  c = 5;
  // zapíše do paměti uvnitř proměnné d ale proměnná hodnota d se nezměnila je to stále pointer na tu samou adresu
  *d = 5;
  int f = 5;
  // změnily jsme hodnotu proměnné e ale nezměnily jsme obsah adresy kam e ukazuje
  e = &f;
}

int main() {
  int a = 0;
  int b = 0;
  int *c = &a;
  foo(a, &b, c);
  printf("%d, %d, %d\\n", a, b, *c);
  return 0;
}

Tento program vypíše:

0, 5, 0

Array

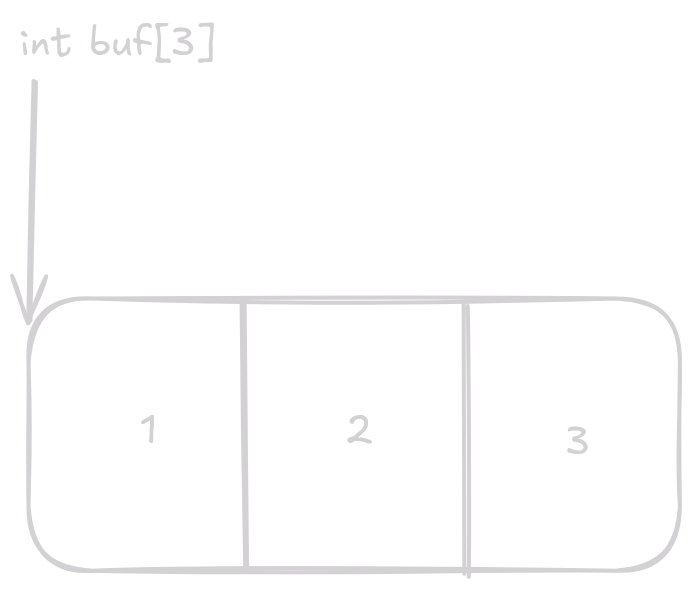
Array nebo pole je segment v paměti kde jsou za sebou jednotlivé hodnoty. Proměnná int buf[3] drží pointer na segment v paměti kde jsou dané hodnoty.

int main() {
  int buf[3] = {1, 2, 3};
  return 0;
}

Rozdíl mezi předchozím a následujícím příkladem je, že v prvním případě je známá velikost arraye při kompilaci a buf bude ukazovat na stack to je důvod proč je velikost součástí typu. V dalším případě je buf pointer na heap a není při kompilaci známá jeho velikost typ proměnné buf je tedy pouze int *buf.

int main() {
  char *buf = malloc(sizeof(char) * 3);
  return 0;
}

Struct

Struct nebo struktura je definované uspořádání v paměti. Můžeme nadefinovat strukturu s více poli různé (ale známé) velikosti.

struct triplet {
  int a;
  long b;
  char *c;
};

Struct poté inicializujeme takto

int main() {
  struct triplet t = {
      .a = 1,
      .b = 2,
      .c = "hello",
  };
  return 0;
}

Pokud chceme referencovat struct sám v sobě vypadá to takto.

struct Node {
  int data;
  struct Node *next;
};

Definice typů

Definice typů nám dovolují pojmenovávat tvar

typedef short unsigned int u8;

Máme možnost vytvořit typ pro anonymní struct:

typedef struct {
  int a;
  int b;
} example_t;

Tato část definuje tvar našeho typu a example_t je pak jméno našeho typu:

struct {
  int a;
  int b;
}

Někdy chceme zadefinovat typ o tvaru, který referencuje sám sebe:

typedef struct Node {
  int data;
  struct Node *next;
} Node;

Nejdříve zadefinujeme struct Node poté celý typ pojmenujeme Node.

Manuálové stránky

Manuálové stránky nebo man pages obsahují dokumentaci funkcím v C. Pokud nevíte, co nějaká funkce dělá je vysoce pravděpodobné, že o ní existuje man page. Zadejte do svého terminálu man 3 <jméno funkce> kde se vám poté snad zobrazí více informací. 3 znamená že chcete hledat v manuálu knihoven. Pro více informací použijte man man.

Linked List

Linked list je jedna z nejzákladnějších datových struktur. Je to nejjednodušší způsob, jak vytvořit list, kterému se mění délka. Základním stavebním blokem linked listu je Node který v sobě má data a pointer na další Node.

Linked list má užitečnější variantu doubly linked list kde každá Node má pointer na další a předchozí Node.

Dále budu mluvit o této variantě linked listu, protože je výrazně užitečnější než single linked list. Kdykoliv z nějakého důvodu budete chtít používat linked list budete pravděpodobně chtít použít doubly linked list, a ne single linked list. Dále proto budu říkat jen linked list, ale budu tím myslet doubly linked list

Reprezentace Linked Listu

Pro optimální zacházení s linked listem máme struct co nám drží první a poslední prvek v listu. Toto nám značně zjednoduší zacházení s listem a sníží časovou náročnost některých operací.

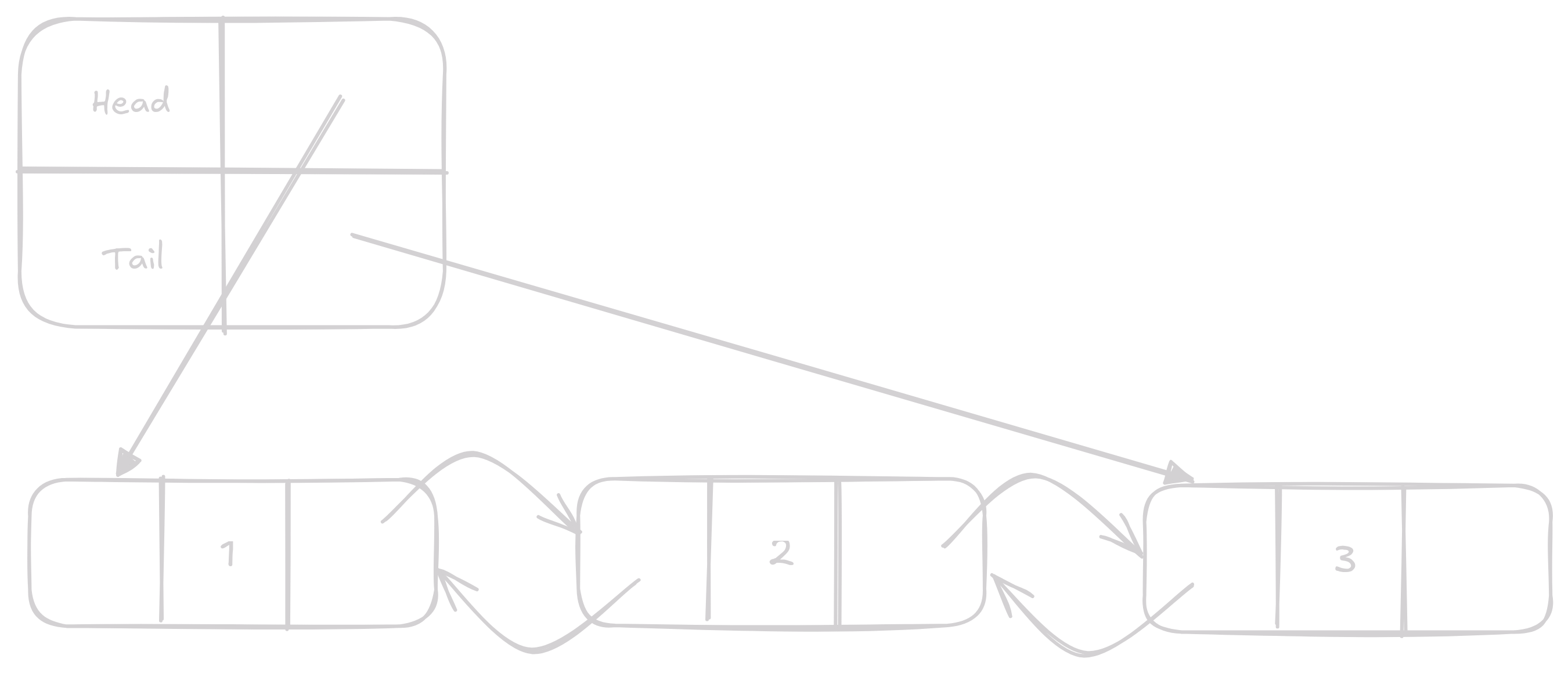
Pro zjednodušení jedné operace ještě budeme držet délku linked listu, o tom, ale později.

V C náš linked list vypadá takto

typedef struct Node {
  int data;
  struct Node *next;
  struct Node *prev;
} Node;

typedef struct {
  Node *head;
  Node *tail;
  size_t length;
} DoublyLinkedList;

Uživatel bude mít DoublyLinkedList a samotný linked list se bude skládat z sebe navazujících Node.

Operace na Doubly Linked List

V této sekci projdeme, jaké operace na doubly linked listu jsou a jaké mají časové náročnosti.

Append a Prepend

Nejzákladnější operace, které nám dovolují přidávat do Listu prvky. Mají časovou náročnost O(1) tedy konstantní. Jediné co se stane je, že změníme head nebo tail Node v našem structu a pro bývalý konec nebo začátek změníme jeho další nebo předchozí Node.

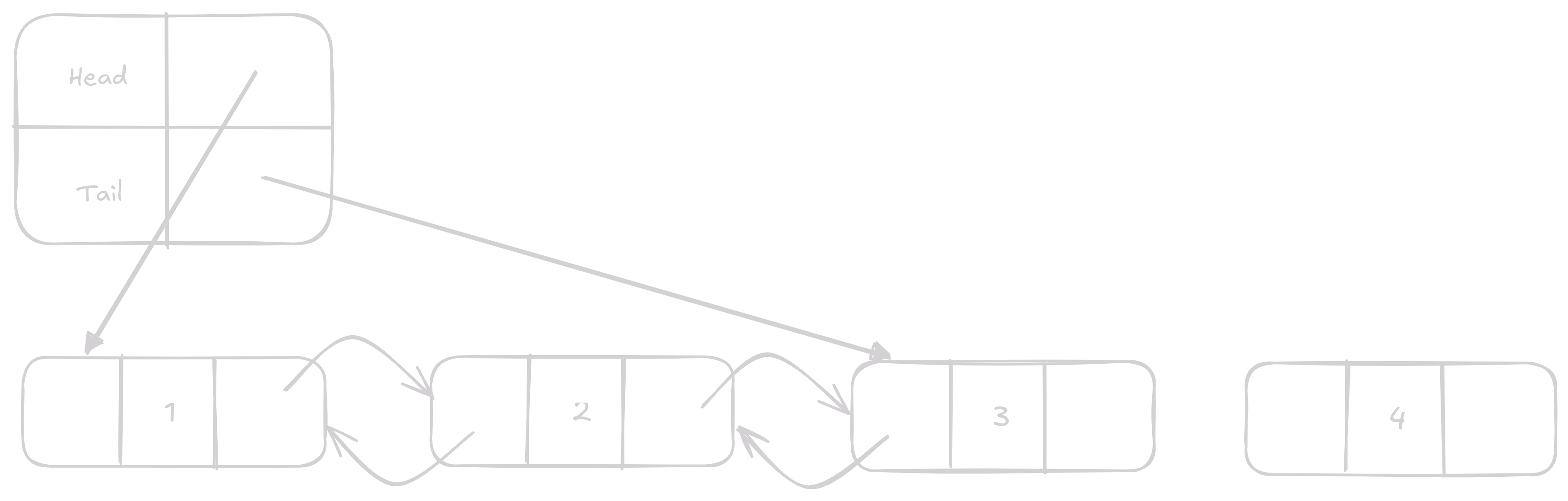
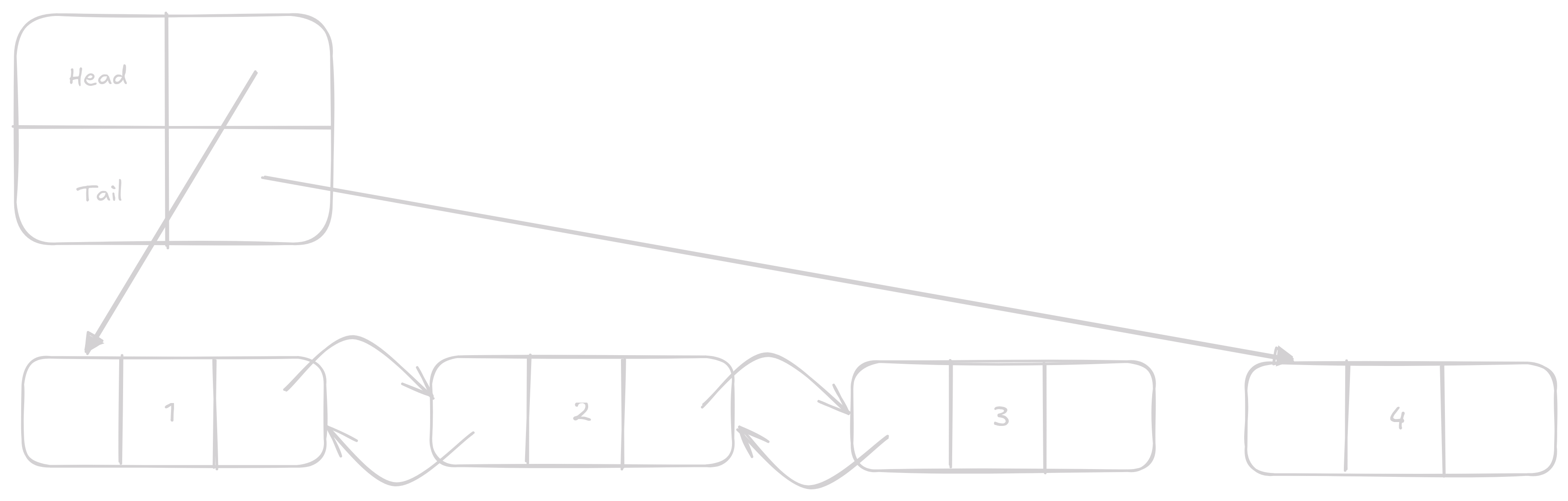
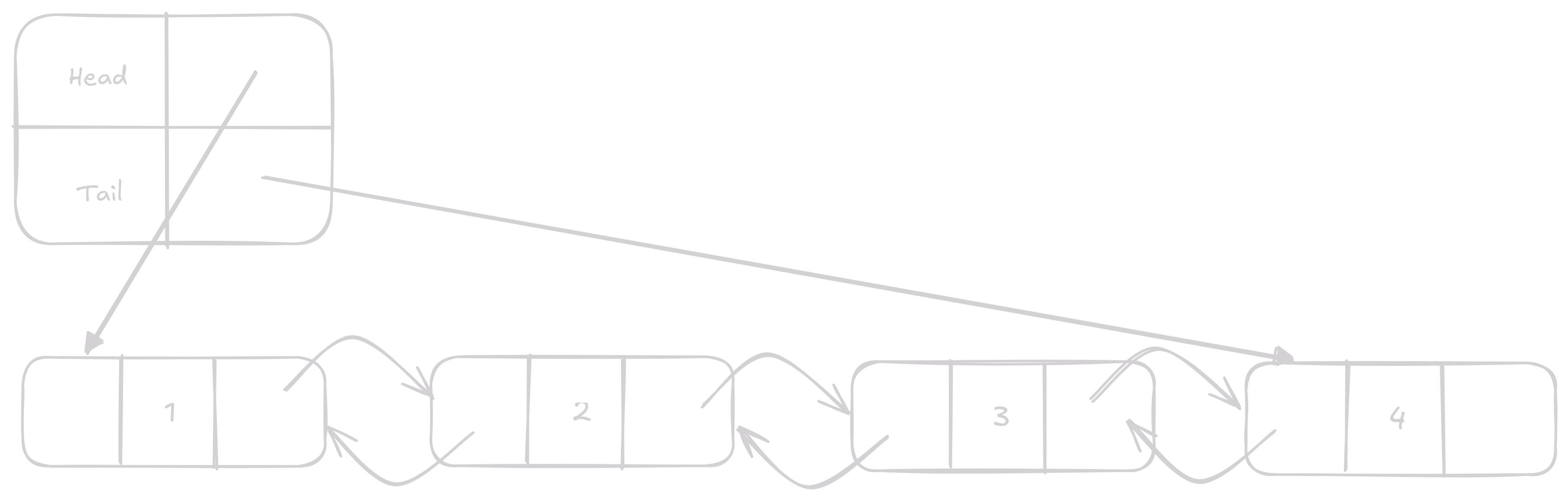
Pop a Shift

Toto je opak append a prepend operace. V případě pop nastavíme tail na prev momentálního tail a v případě shift nastavíme head na next momentálního head. Jedná se O(1) konstantní operace.

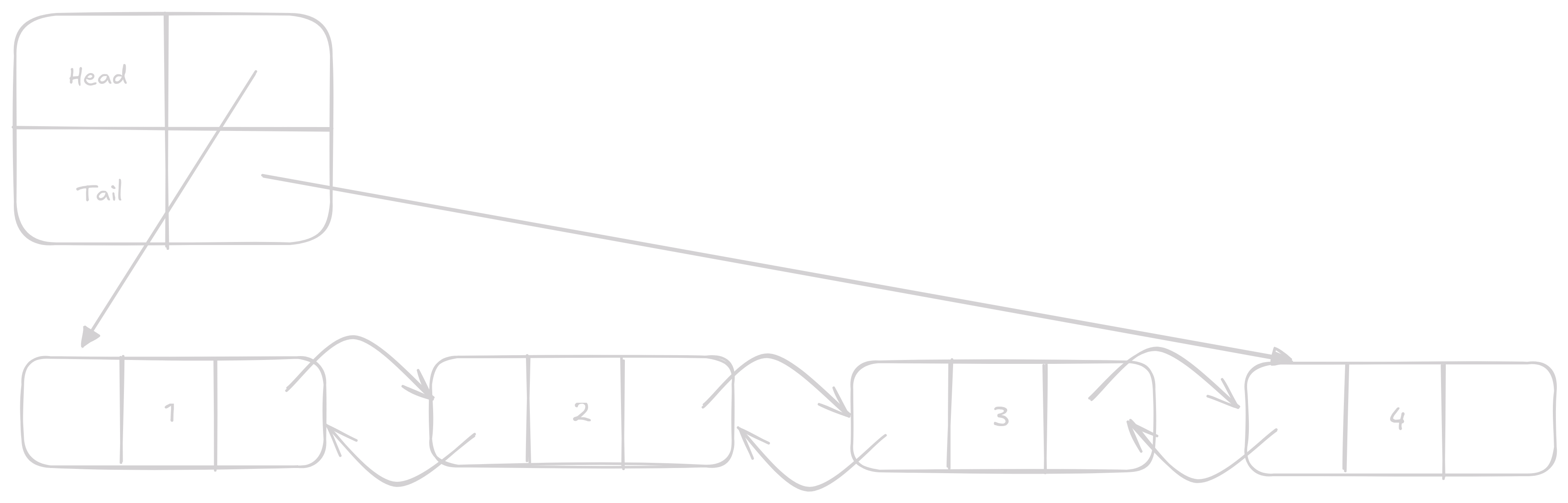
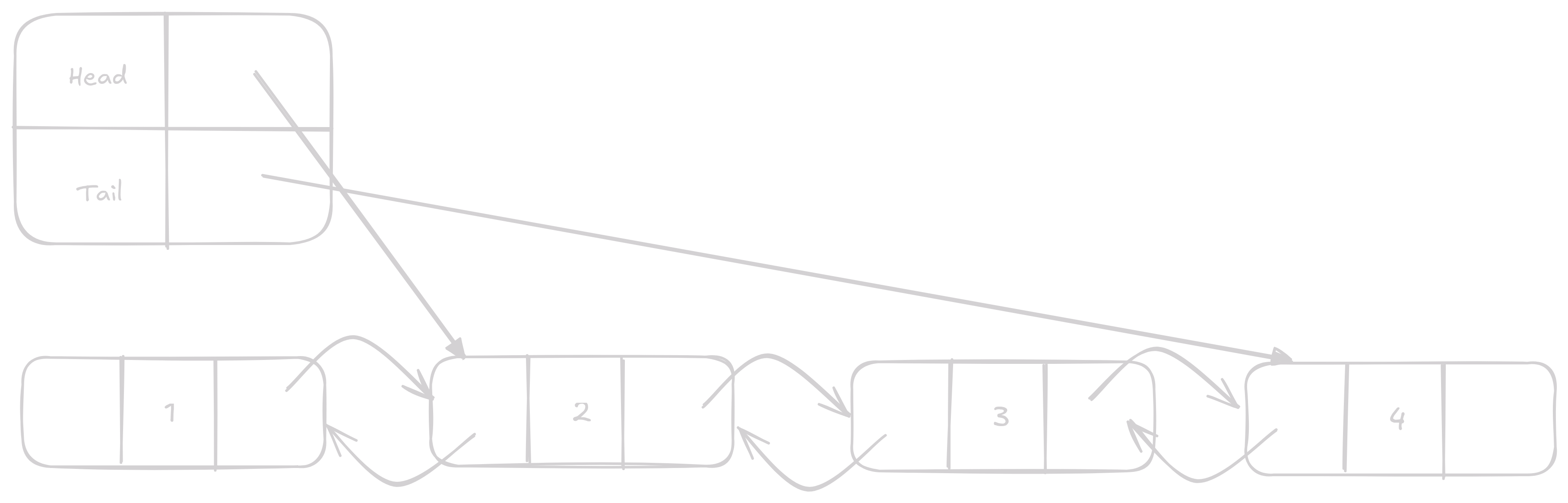
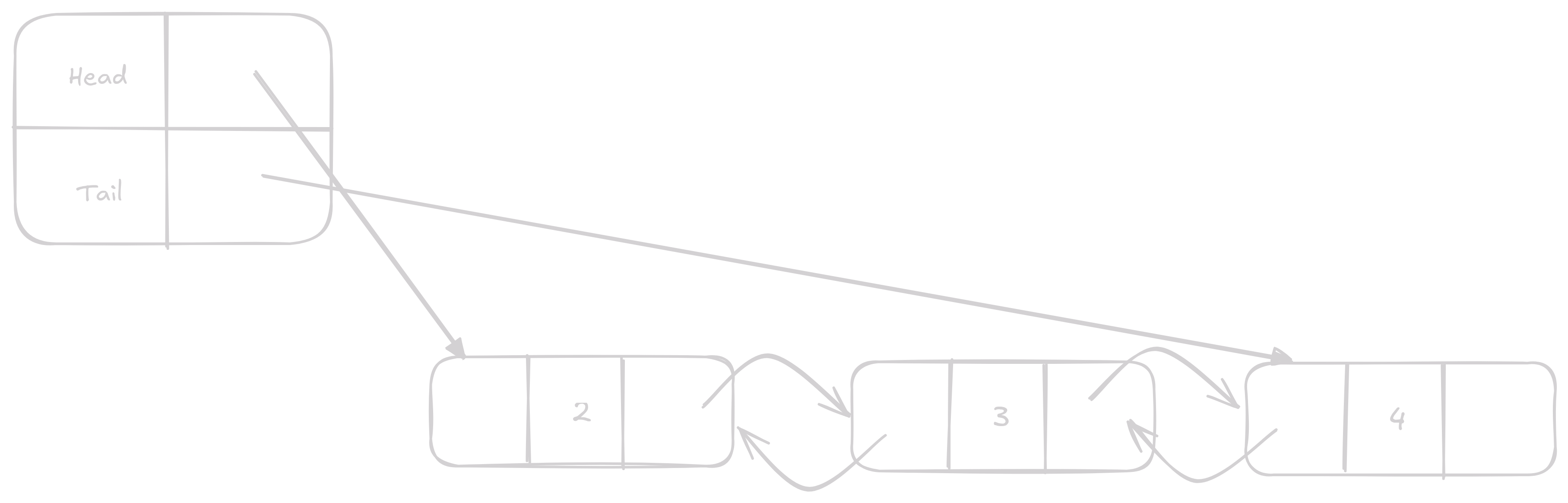
Insert

Insert má dvě varianty, insert před a po Node. Jediné, čím se liší insert před a po Node je v tom, jak se mění next a prev. Při insert po se musí vyměnit next za Node který chceme insertovat a původnímu next musíme nastavit prev na insertovaný Node. Taky musíme zkontrolovat jeslti není potřeba změnit head pokud insertujeme před první Node a tail pokud za poslední. Opět se jedná o O(1) operaci s konstatním časem.

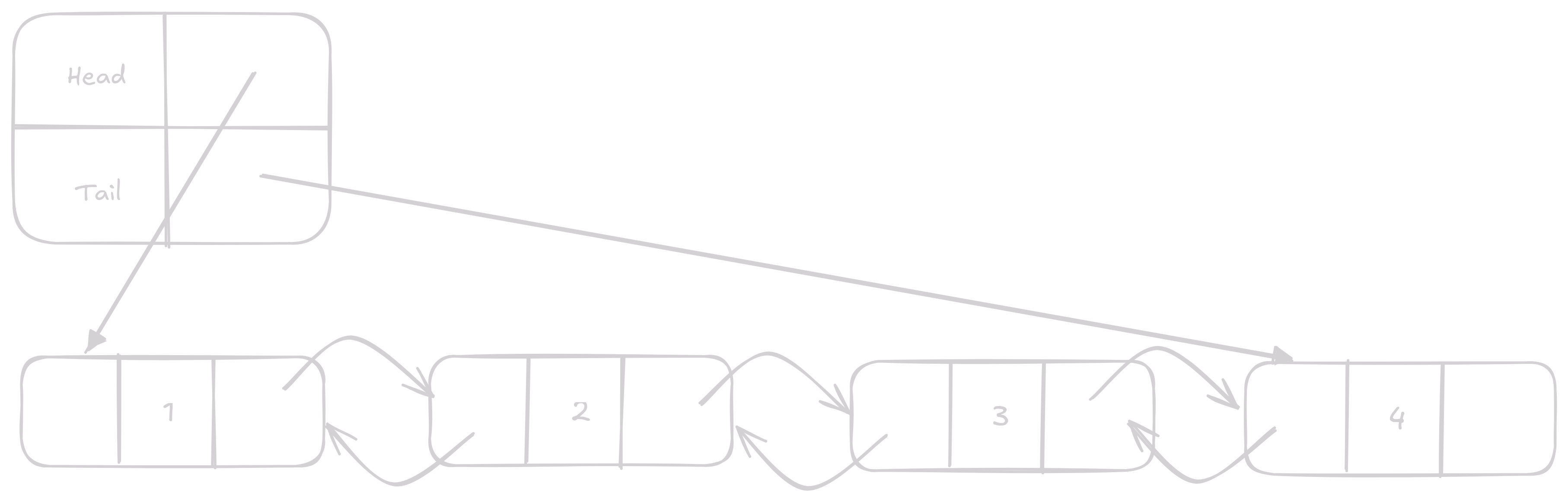
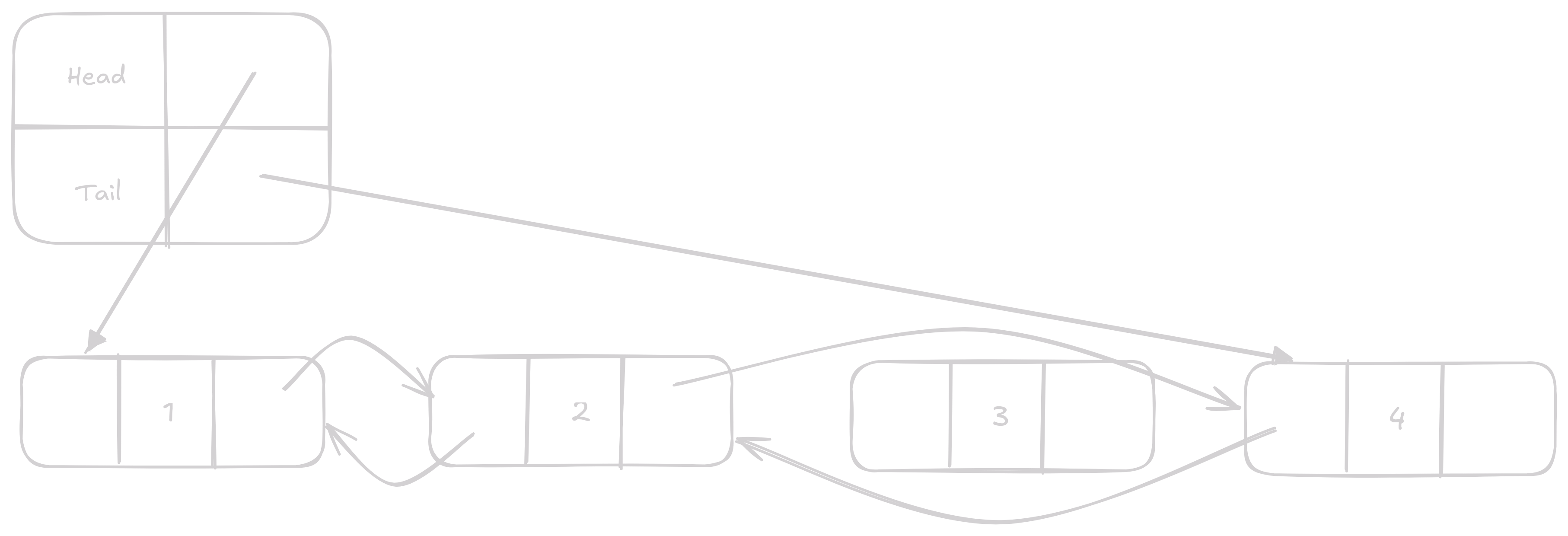
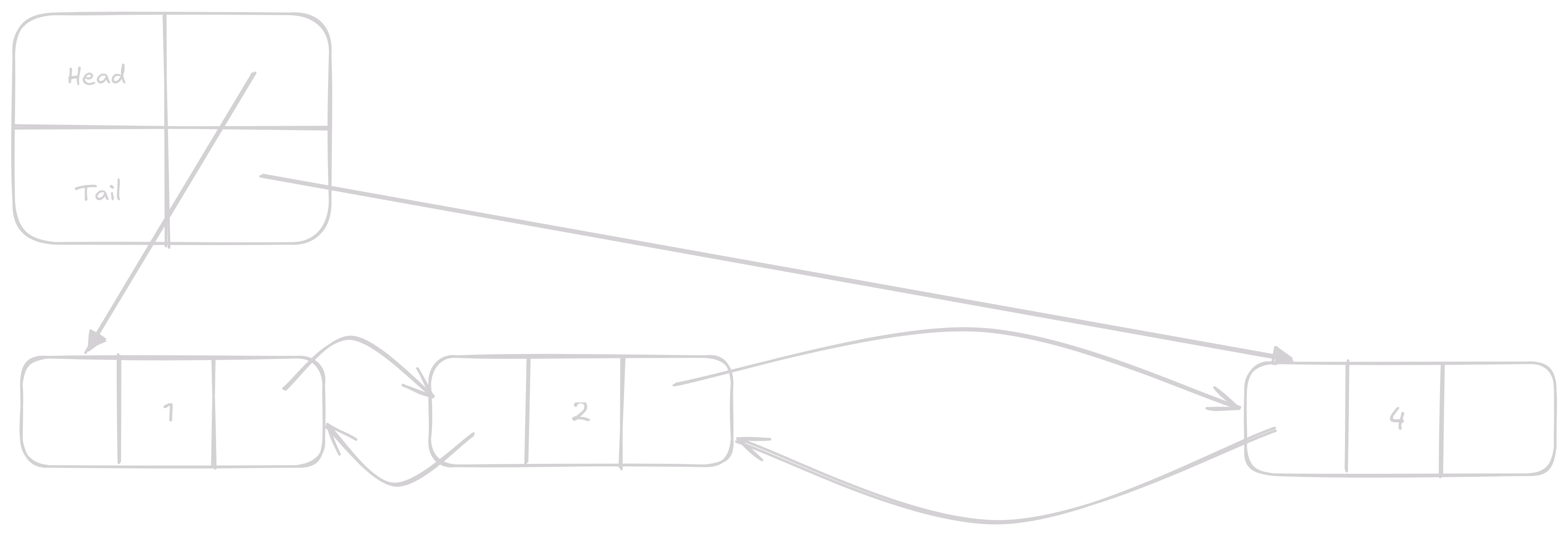
Remove

Remove odstraní vybraný Node. Co efektivně uděláme je, že nastavíme vezmeme next Node kterou chceme odstranit a nastavíme mu prev na prev naší vybrané Node. To samé potom uděláme pro prev. A něco mi říká že vás nepřekvapí, že to je operace s konstantním časem O(1).

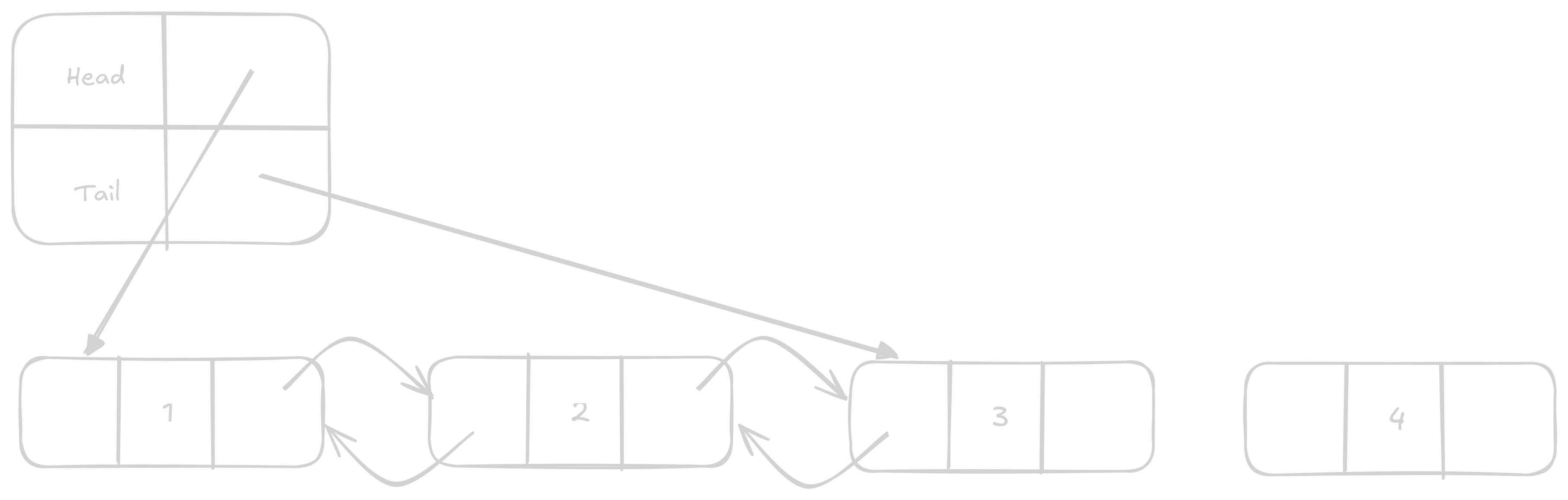
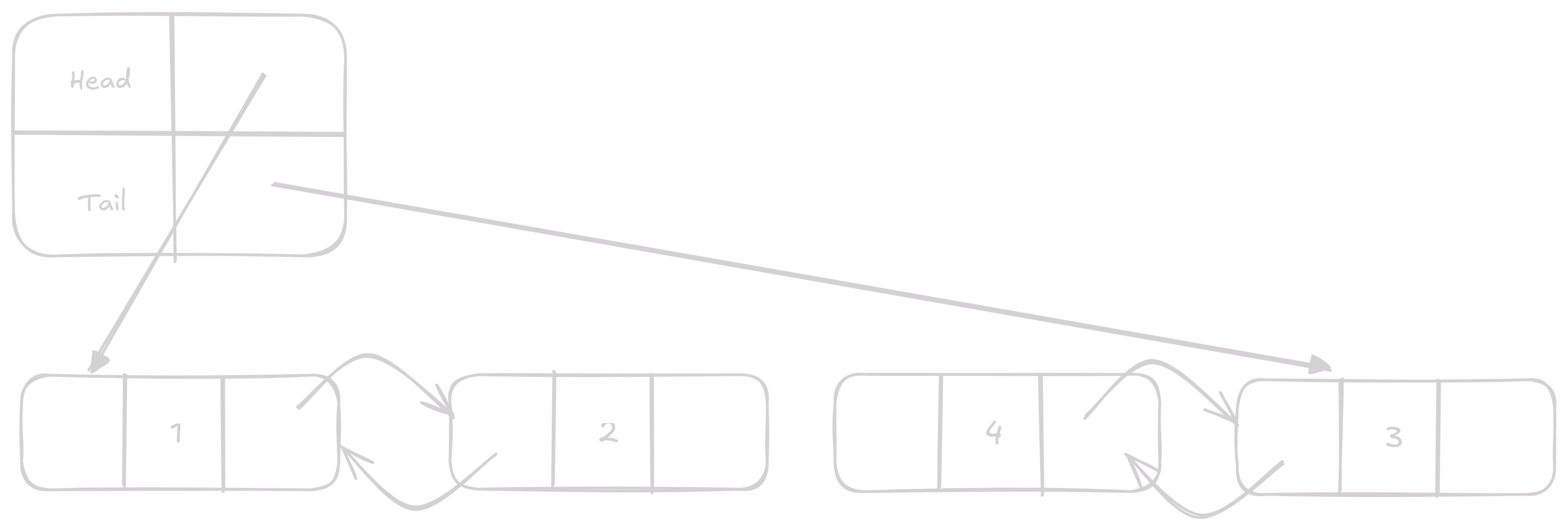
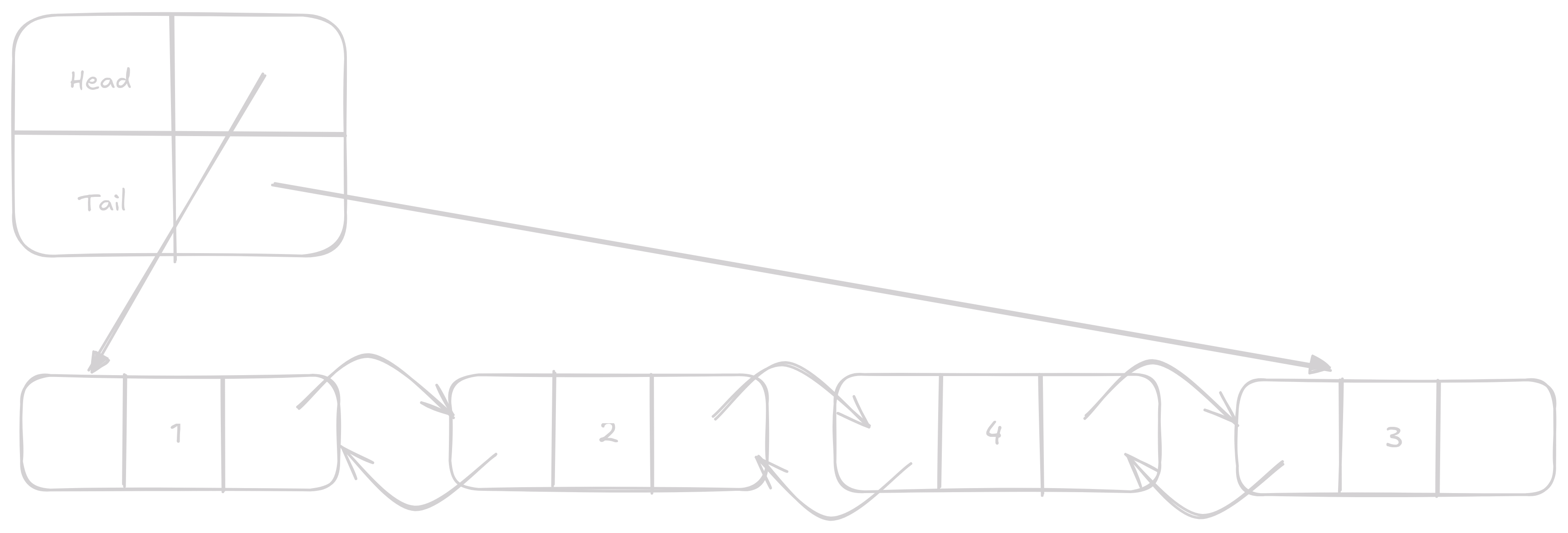
N-tý prvek

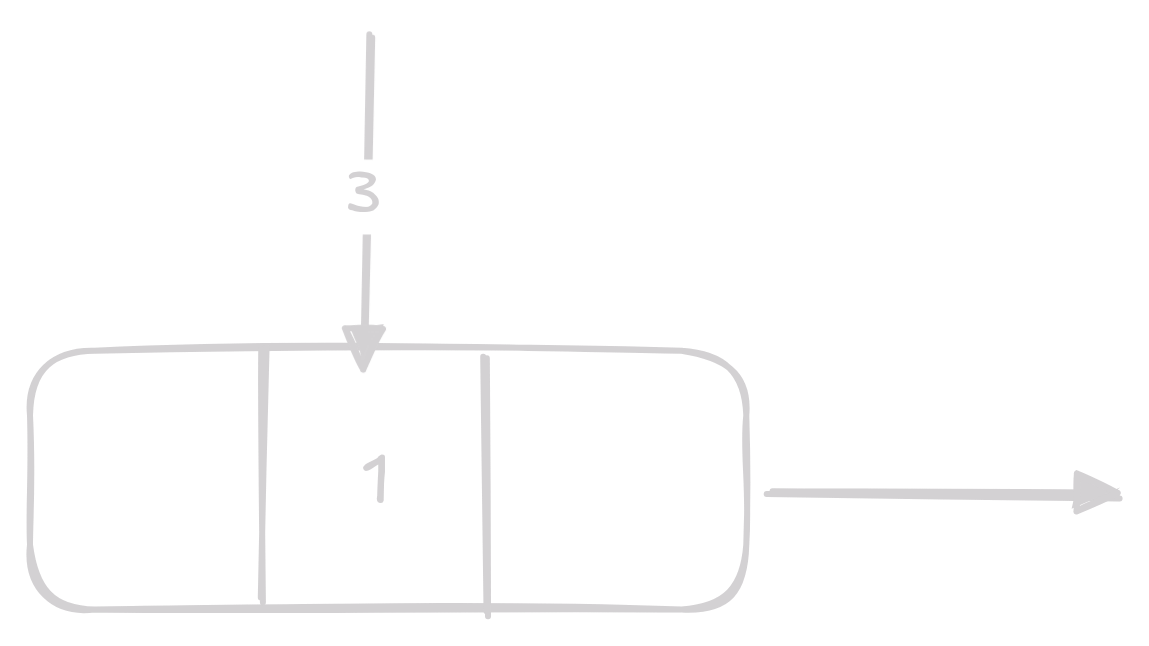
Zatím všechny operace, které jsem na linked list ukázal měli konstantní čas to se, ale změní tady. Jediný způsob, jak získat N-tý prvek v linked listu je buď odzadu nebo předu projít všechny prvky doku se neodstaneme na N-tý prvek. Jediná optimalizace, kterou můžeme používat je, že držíme délku listu a spočítáme jeslti je rychlejší jíd od předu nebo od zadu. Tak i tak bude časová náročnost této operace O(n) vzhledem k počtu prvků.

Získání 4. prvku v linked listu by vypadalo takto:

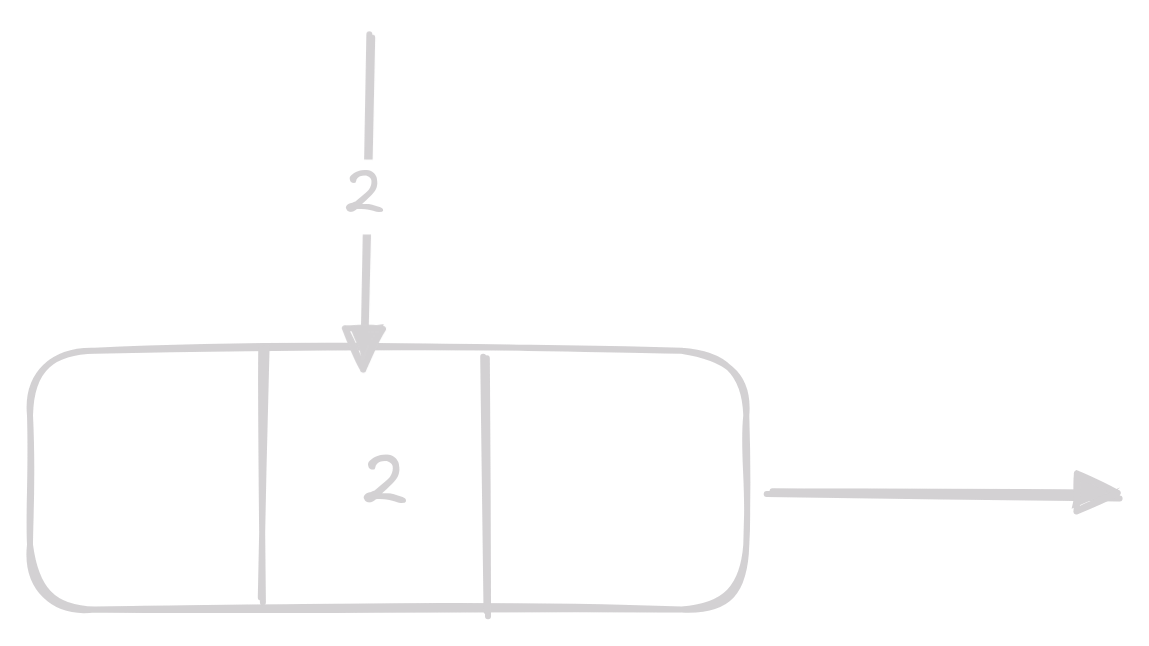
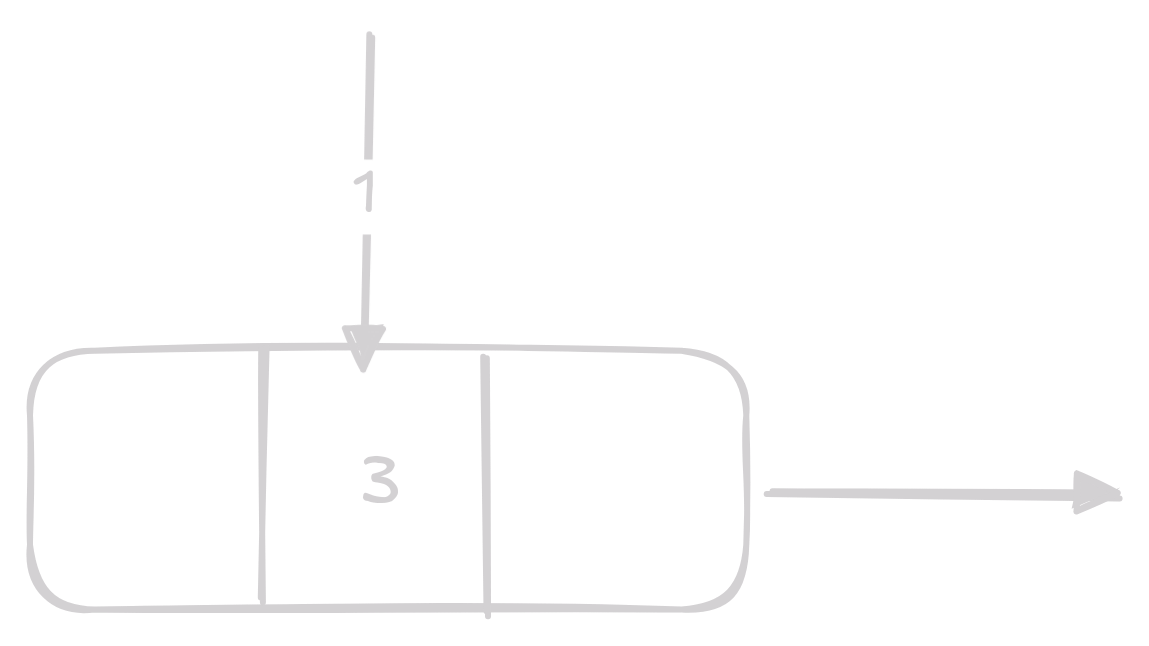
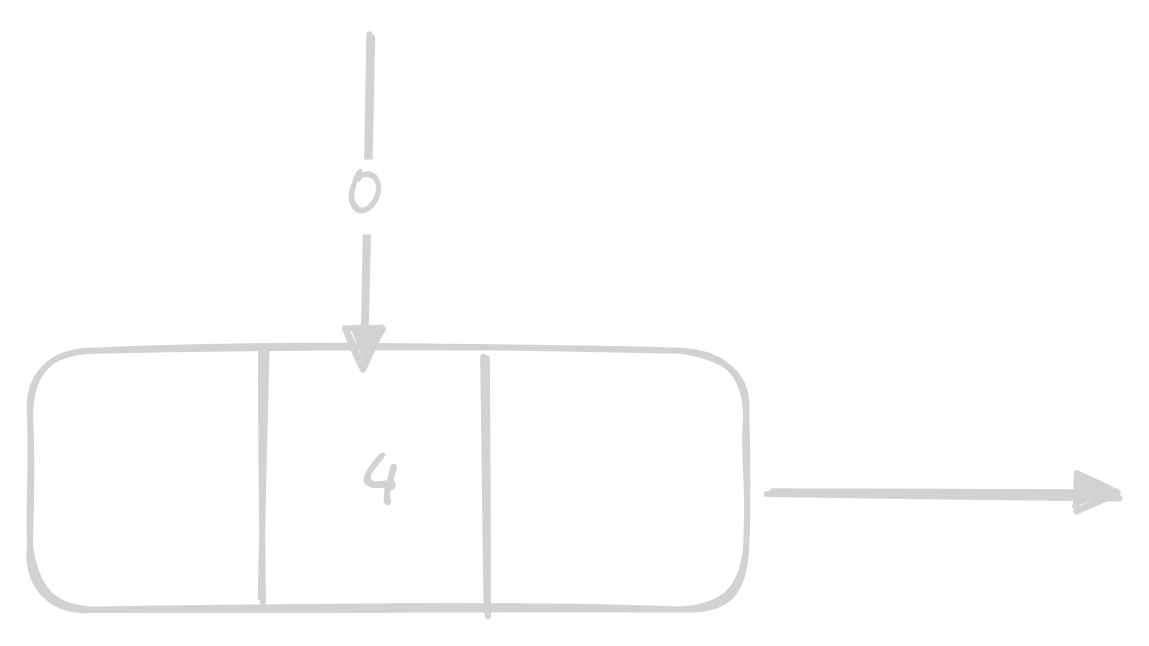
Implementace Linked Listu

V této sekci projdeme implementaci linked listu v jazyce C. Pokud si chcete kompletní implementaci projít sami můžete si zde stáhnout header file a zde samotný C soubor.

První potřebujeme samotnou datovou strukturu. Tu jste již viděli výše:

typedef struct Node {
  int data;
  struct Node *next;
  struct Node *prev;
} Node;

typedef struct {
  Node *head;
  Node *tail;
  size_t length;
} DoublyLinkedList;

Další, co si budeme chtít zadefinovat jsou errory, co budeme používat.

typedef enum {
  LIST_OK,
  LIST_ERROR_EMPTY,
  LIST_ERROR_INVALID_INDEX,
  LIST_ERROR_MEMORY_ALLOCATION,
  LIST_ERROR_NULL_POINTER
} ListError;

Naše funkce budou operovat tak, že vždy budou brát jako argument pointer na DoublyLinkedList a budou vracet ListError. Pokud funkce bude potřebovat nějaká data vrátit bude brát pointer do kterého data uloží.

Inicializace

První funkce, co náš linked list potřebuje je init funkce, která struct nastaví na validní data. V tomto případě je to jednoduché head a tail stačí nastavit na NULL a length na 0.

ListError list_init(DoublyLinkedList *list) {
  if (list == NULL) {
    return LIST_ERROR_NULL_POINTER;
  }
  list->head = NULL;
  list->tail = NULL;
  list->length = 0;
  return LIST_OK;
}

Append a Prepend

Append a prepend, jak je popsáno výše jen mění head a tail našeho listu. Nejdříve je třeba alokovat prostor pro novou Node na heapu a poté musíme zkontrolovat, že list není prázdný.

ListError list_append(DoublyLinkedList *list, int data) {
  if (list == NULL) {
    return LIST_ERROR_NULL_POINTER;
  }
  Node *new_node = (Node *)malloc(sizeof(Node));
  if (new_node == NULL) {
    return LIST_ERROR_MEMORY_ALLOCATION;
  }

  new_node->data = data;
  new_node->next = NULL;

  // Pokud je list prázdný nový Node je head i tail listu
  if (list->tail == NULL) {
    new_node->prev = NULL;
    list->head = new_node;
    list->tail = new_node;
  } else {
    // next momentálního tail bude nový Node a tail se nastaví na nový Node
    new_node->prev = list->tail;
    list->tail->next = new_node;
    list->tail = new_node;
  }

  list->length++;
  return LIST_OK;
}

Prepend funguje velmi podobně jen se prohazuje role head a tail.

ListError list_prepend(DoublyLinkedList *list, int data) {
  if (list == NULL) {
    return LIST_ERROR_NULL_POINTER;
  }
  Node *new_node = (Node *)malloc(sizeof(Node));
  if (new_node == NULL) {
    return LIST_ERROR_MEMORY_ALLOCATION;
  }

  new_node->data = data;
  new_node->prev = NULL;

  if (list->head == NULL) {
    new_node->next = NULL;
    list->head = new_node;
    list->tail = new_node;
  } else {
    new_node->next = list->head;
    list->head->prev = new_node;
    list->head = new_node;
  }

  list->length++;
  return LIST_OK;
}

Pop a Shift

Pop a shift provedou opak append a prepend. Vzhledem k tomu, že uživatel bude chtít data, která byla z listu odstraněna bude jeden z argumentů pointer, do kterého se data uloží. Zároveň nesmíme zapomenout uvolnit paměť odstraněné Node

ListError list_pop(DoublyLinkedList *list, int *data) {
  if (list == NULL) {
    return LIST_ERROR_NULL_POINTER;
  }
  if (list->tail == NULL) {
    return LIST_ERROR_EMPTY;
  }

  Node *temp = list->tail;
  *data = temp->data;

  // Pokud má tail prev nový tail bude prev momentálního tail
  if (list->tail->prev) {
    list->tail = list->tail->prev;
    // Nezapomeňme, že poslední Node nemá next
    list->tail->next = NULL;
  } else {
    // Pokud je list prázdný vynulujeme head i tail
    list->head = NULL;
    list->tail = NULL;
  }

  free(temp);
  list->length--;
  return LIST_OK;
}

ListError list_shift(DoublyLinkedList *list, int *data) {
  if (list == NULL) {
    return LIST_ERROR_NULL_POINTER;
  }
  if (list->head == NULL) {
    return LIST_ERROR_EMPTY;
  }

  Node *temp = list->head;
  *data = temp->data;

  if (list->head->next) {
    list->head = list->head->next;
    list->head->prev = NULL;
  } else {
    list->head = NULL;
    list->tail = NULL;
  }

  free(temp);
  list->length--;
  return LIST_OK;
}

Insert

Insert před a po je velmi podobný jako append a prepend. Hlavním rozdílem je, že nekontrolujeme, zda je list prázdný, protože očekáváme, že obsahuje alespoň Node za nebo před který máme insertovat.

ListError list_insert_after(DoublyLinkedList *list, Node *prev_node, int data) {
  if (list == NULL || prev_node == NULL) {
    return LIST_ERROR_NULL_POINTER;
  }
  Node *new_node = (Node *)malloc(sizeof(Node));
  if (new_node == NULL) {
    return LIST_ERROR_MEMORY_ALLOCATION;
  }

  new_node->data = data;
  new_node->next = prev_node->next;
  new_node->prev = prev_node;

  if (prev_node->next != NULL) {
    prev_node->next->prev = new_node;
  } else {
    // Pokud next prev_node byl NULL znamená to, že byla poslední a inserted Node
    // je tedy nový tail
    list->tail = new_node;
  }

  prev_node->next = new_node;
  list->length++;
  return LIST_OK;
}

ListError list_insert_before(DoublyLinkedList *list, Node *next_node, int data) {
  if (list == NULL || next_node == NULL) {
    return LIST_ERROR_NULL_POINTER;
  }

  Node *new_node = (Node *)malloc(sizeof(Node));
  if (new_node == NULL) {
    return LIST_ERROR_MEMORY_ALLOCATION;
  }

  new_node->data = data;
  new_node->prev = next_node->prev;
  new_node->next = next_node;

  if (next_node->prev != NULL) {
    next_node->prev->next = new_node;
  } else {
    list->head = new_node;
  }

  next_node->prev = new_node;
  list->length++;
  return LIST_OK;
}

Remove

Remove je podobný jako pop a shift, ale odstraní jakýkoliv Node z listu. Stejně jako u pop a shift musíme nakonec uvolnit paměť.

ListError list_remove(DoublyLinkedList *list, Node *node) {
  if (list == NULL || node == NULL) {
    return LIST_ERROR_NULL_POINTER;
  }

  if (node->prev != NULL) {
    node->prev->next = node->next;
  } else {
    // pokud node nemá previous znamená to, že je první v listu a jeho next se
    // stává další hlavou
    list->head = node->next;
  }

  if (node->next != NULL) {
    node->next->prev = node->prev;
  } else {
    // to samé co výše u hlavy ale tentokrát u tail
    list->tail = node->prev;
  }

  free(node);
  list->length--;
  return LIST_OK;
}

N-tý prvek

Získání n-tého prvku je jen projetí pomocí for loop skrz všechny prvky. Podle indexu a délky se můžeme rozhodnout, zda půjdeme od head nebo tail. Node poté vrátíme do double pointer. Uživatel pravděpodobně bude chtít zpátky pointer na n-tý Node, abychom mu ho mohly vrátit potřebujeme mít adresu kam uložit pointer. Tedy pointer na pointer.

ListError list_get(DoublyLinkedList *list, size_t index, Node **node) {
  if (list == NULL || node == NULL) {
    return LIST_ERROR_NULL_POINTER;
  }
  if (index >= list->length) {
    return LIST_ERROR_INVALID_INDEX;
  }

  Node *current;
  // Pokud je index před půlkou jdeme od head jinak od tail
  if (index <= list->length / 2) {
    current = list->head;
    for (size_t i = 0; i < index; i++) {
      current = current->next;
    }
  } else {
    current = list->tail;
    for (size_t i = list->length - 1; i > index; i--) {
      current = current->prev;
    }
  }

  // current je pointer na náš node a ten uložíme do místa, které nám dal
  // uživatel
  *node = current;
  return LIST_OK;
}

Free

Poslední, co je potřebuje je po sobě data uklidit. Jediné, co uděláme je, že projedem pomocí while loop všechny Nodes a uvolníme jejich paměť. Samotný DoublyLinkedList *list neuvolňujeme to je problém uživatele.

void list_free(DoublyLinkedList *list) {
  if (list == NULL) {
    return;
  }
  Node *current = list->head;
  Node *next_node;

  while (current != NULL) {
    next_node = current->next;
    free(current);
    current = next_node;
  }
}

Dynamic Array

Někdy také známý jako List nebo Vector. Protože dynamic array je docela dlouhé budu dále používat vector. Vector je jedna z nejverzatilnějších datových struktur, kterou v programování používáme skoro pořád. Jedná se array s dynamickou velikostí tedy array jehož velikost se mění. Array držíme na heapu a pokaždé když do něj přidáme prvek zkontrolujeme, zda je pro něj místo a pokud ne tak array dáme víc místa.

Reprezentace Vectoru

Vector reprezentujeme structem, co drží pointer na náš array, číslo specifikující délku validních dat a kapacitu.

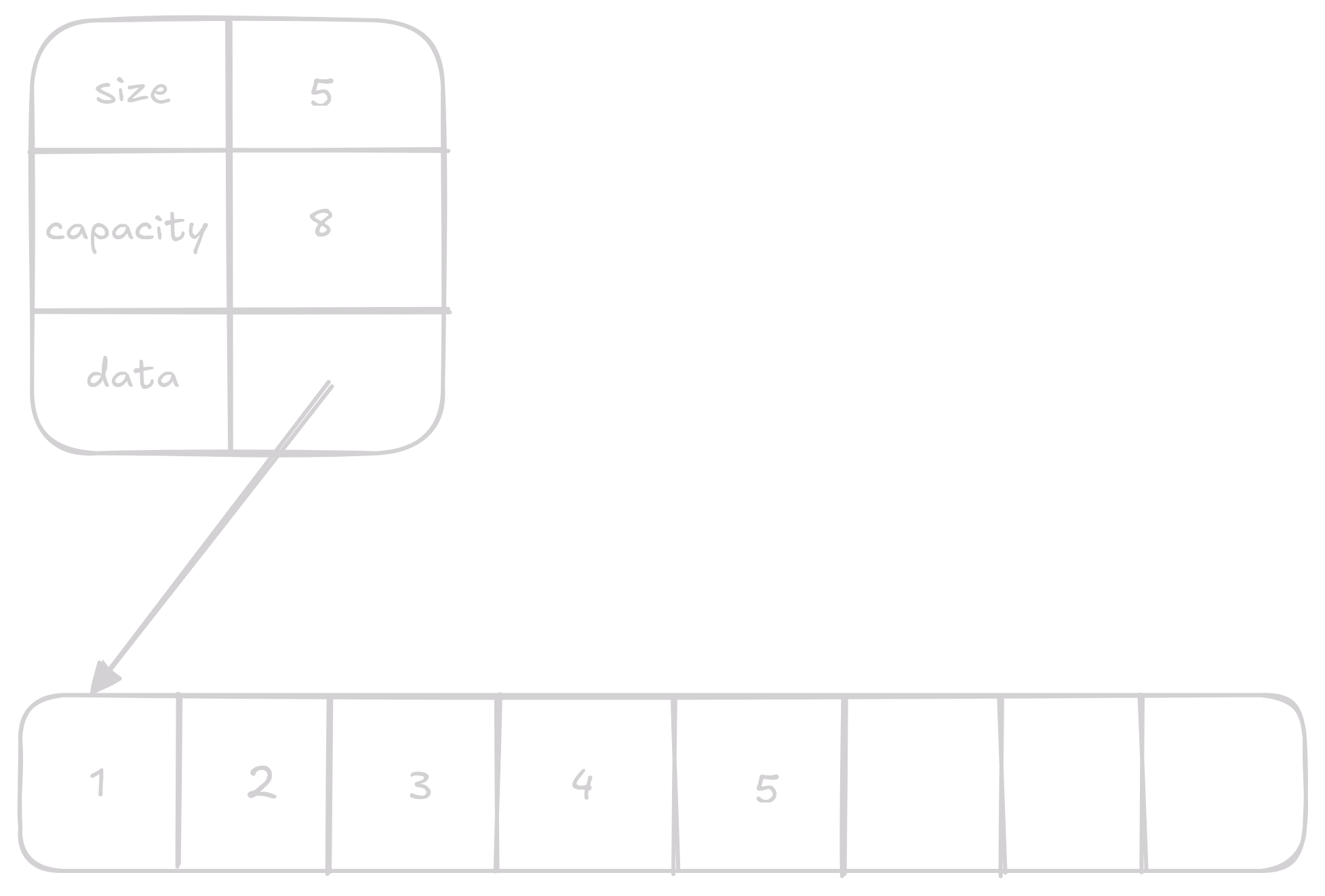
typedef struct {
  int *data;
  size_t size;
  size_t capacity;
} Vector;

Operace na Vectoru

Push

Push přidá prvek na konec vectoru. Pokud stále máme kapacitu kam prvky přidávat stačí na konec validních dat přidat náš prvek. Pokud však je kapacita plná musíme data realokovat a zvětšit kapacitu. To znamená že normálně bude přidání prvku O(1) ale někdy když bude potřeba realokace bude přidání trvat O(n).

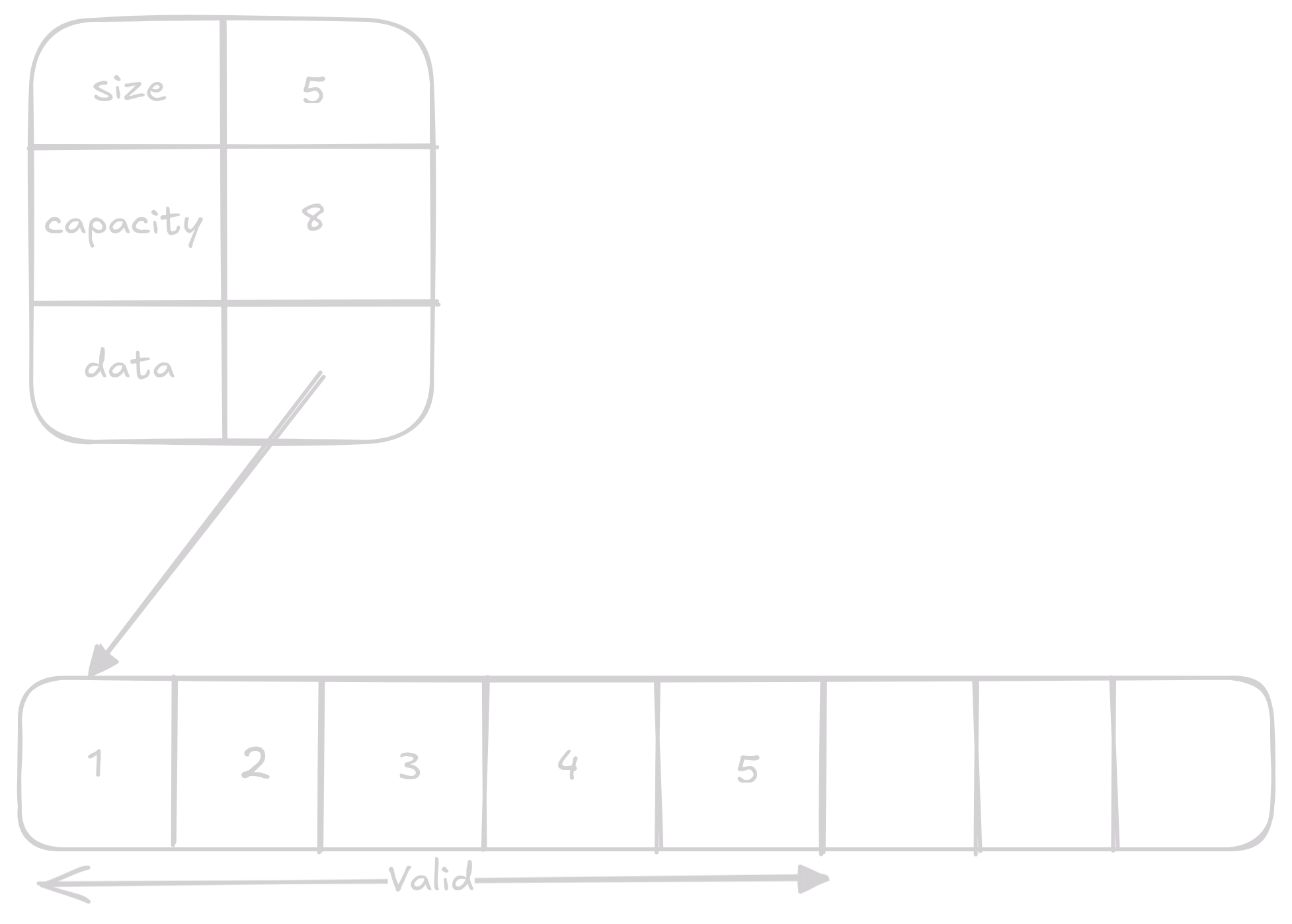
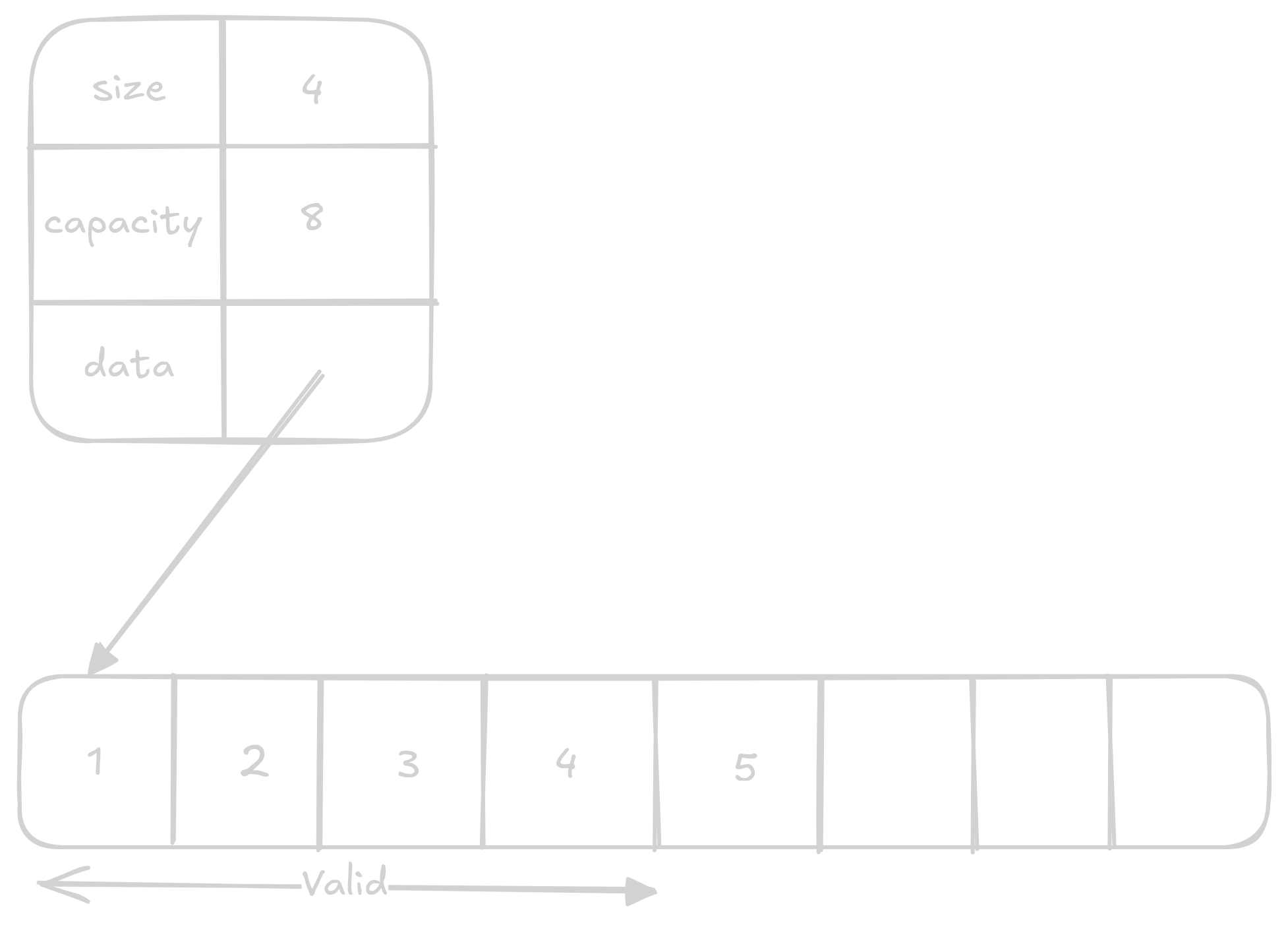
Pop

Pop odstraní poslední prvek z vectoru. V realitě ovšem k žádnému odstraňování nedojde, jediné, co se stane je, že snížíme size který označuje délku validních dat. Při dalším přidání prvku se data prostě přepíšou. Díky tomuto je pop vždy O(1) operace.

Insert

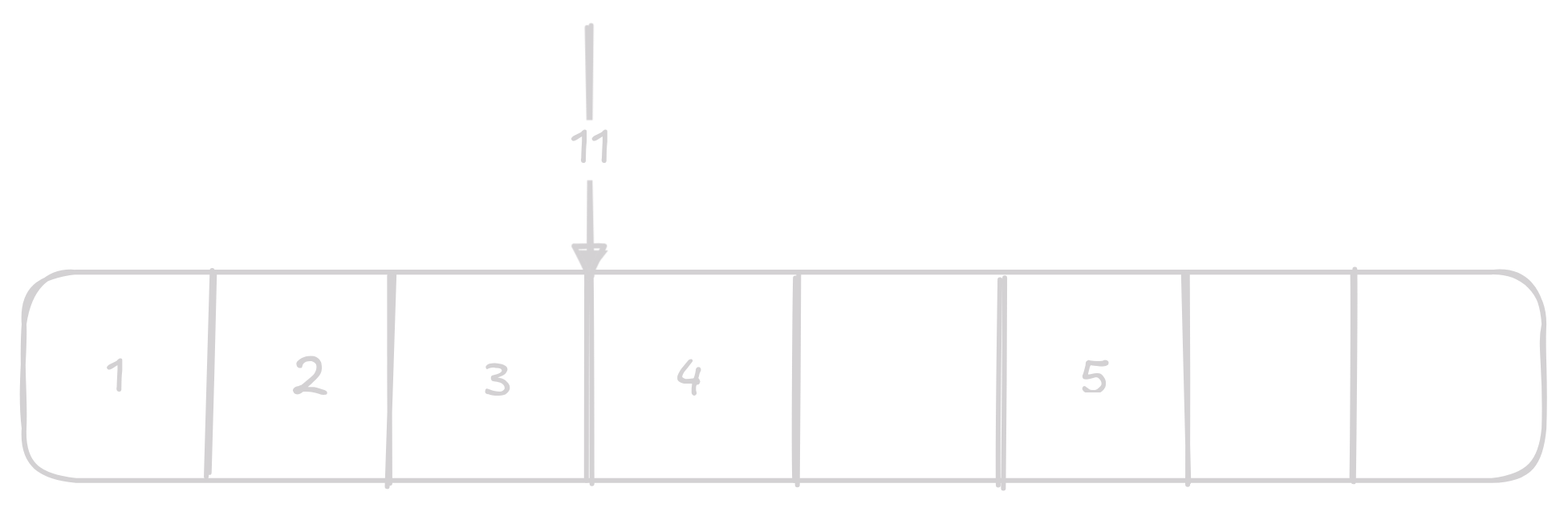
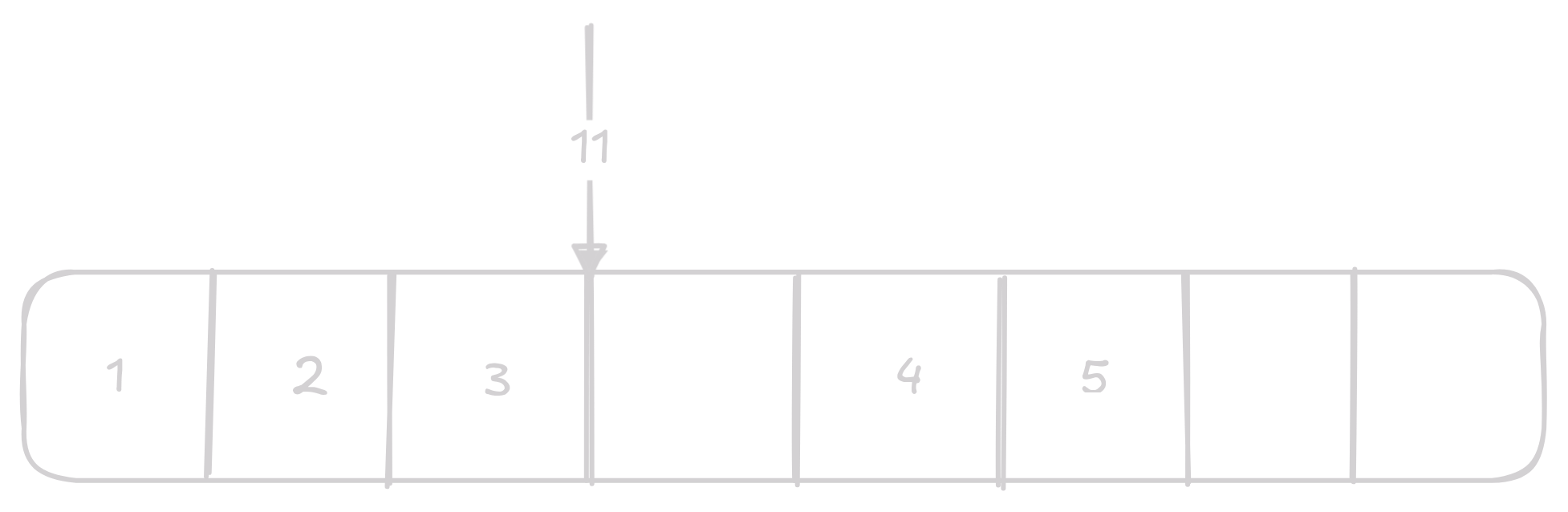
Insert vloží na n-tou pozici ve vectoru prvek. Narozdíl od linked listu ve vectoru nemůžeme jen tak doprostřed vkládat data, protože musíme všechny prvky posunout. Toto vede k tomu, že insert je O(n) operace.

Remove

Remove odstraní n-tý prvek z vectoru. Stejně jako u insert budeme muset všechny prvky přesunout tentokrát je však budeme přesouvat na druhou stranu. Opět se jedná o O(n) operaci.

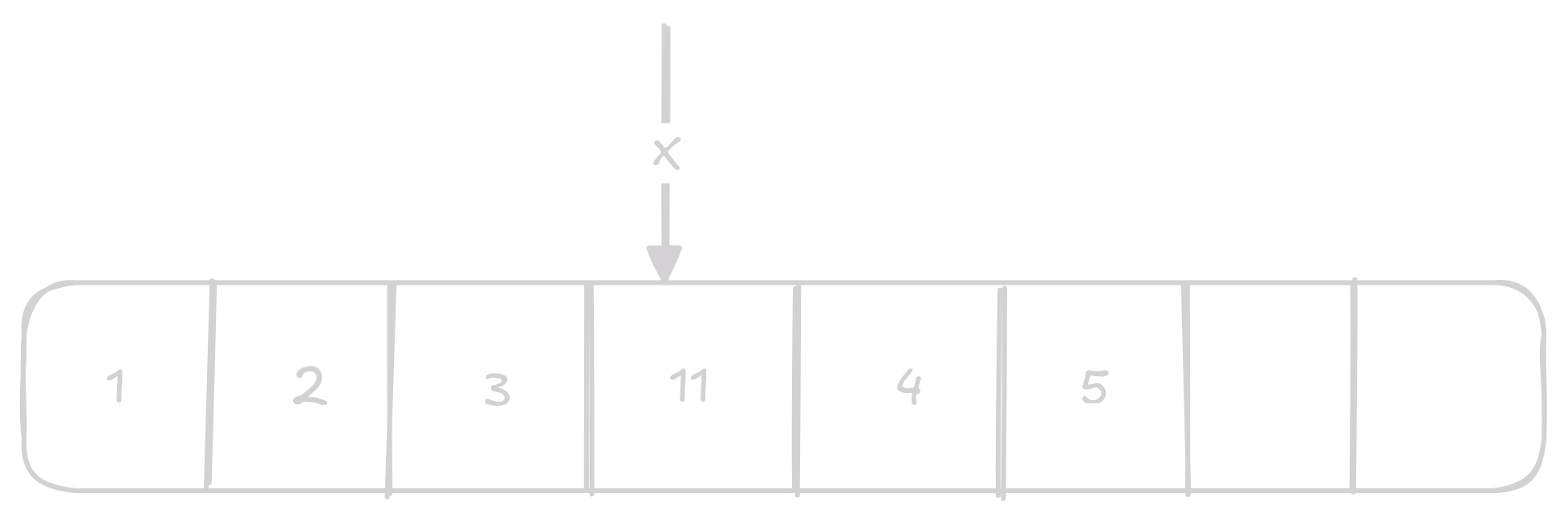
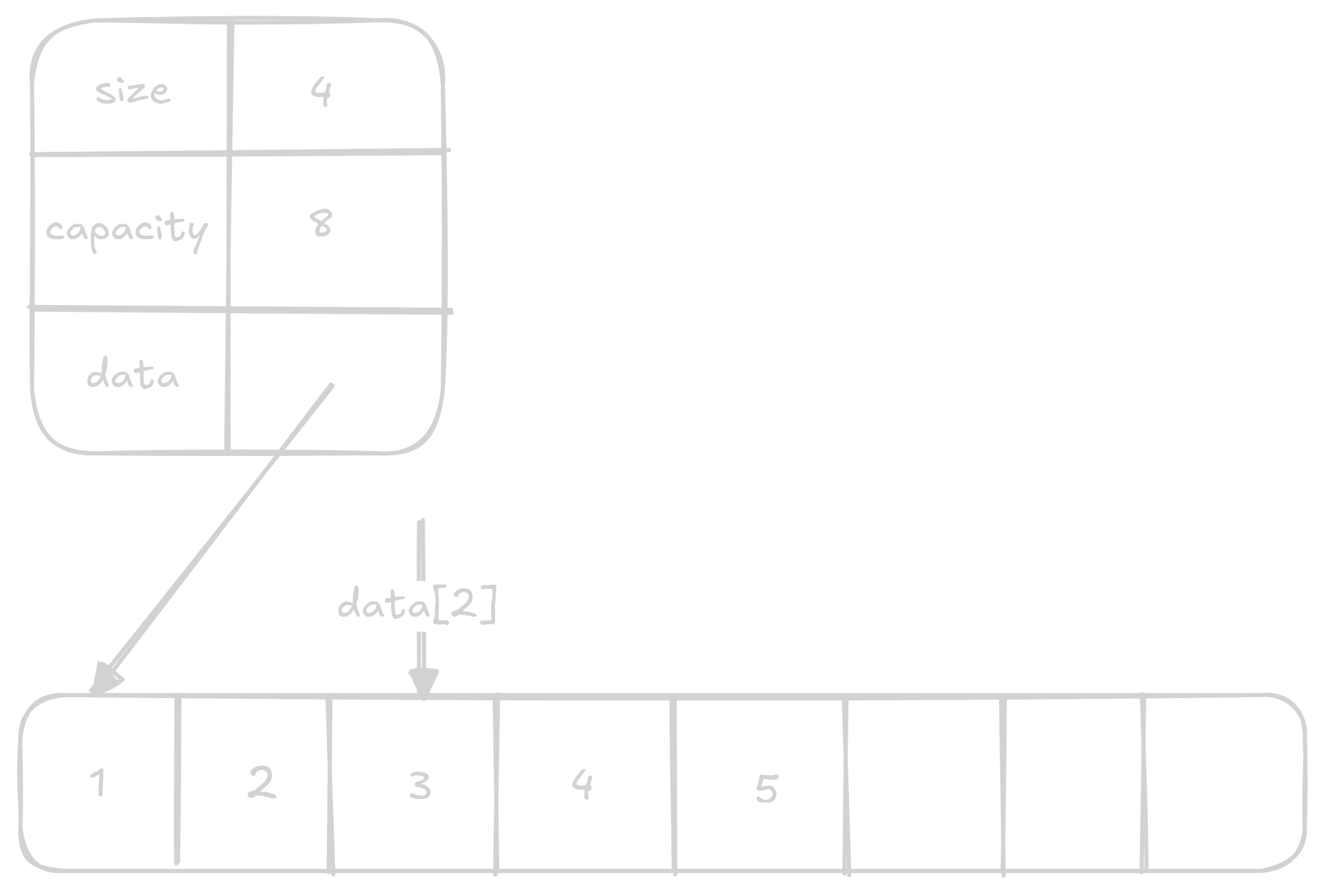
N-tý prvek

Získání n-tého prvku je vyloženě jen indexace do data. Jedná se o O(1) operaci.

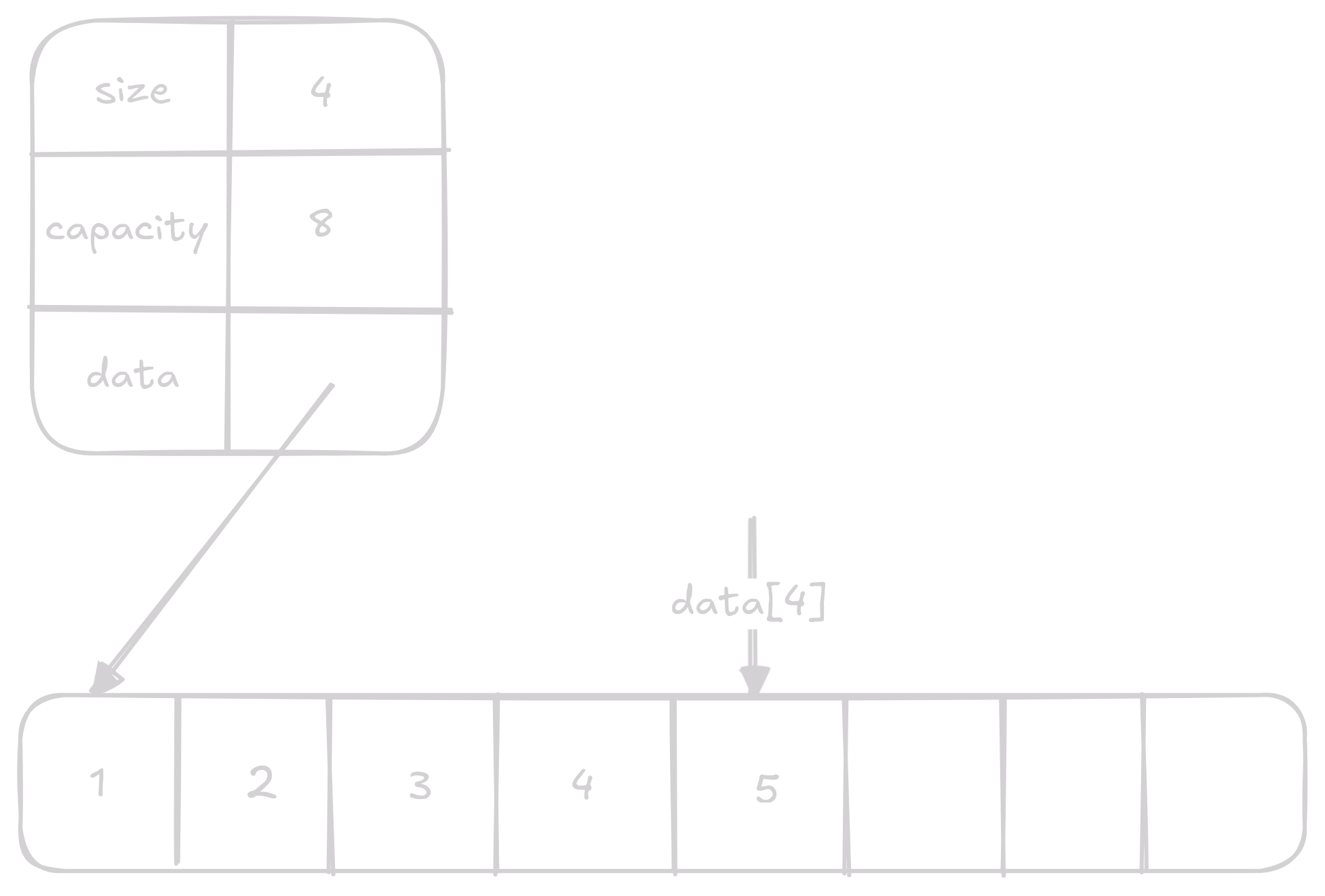
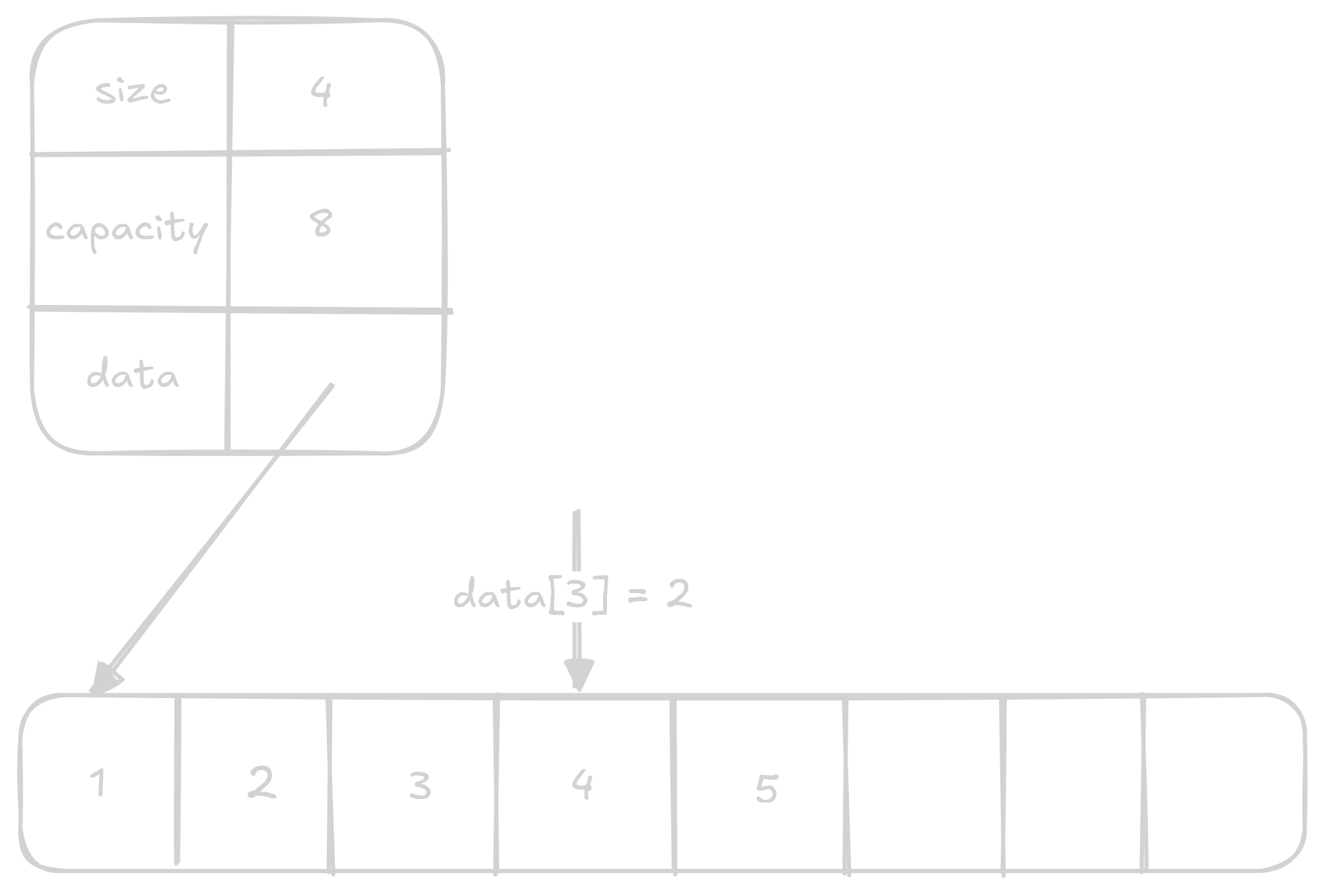
Nastavení N-tého prvku

Nastavení n-tého prvku je jen nastavení indexu v data na nějakou hodnotu. Opět se jedná o O(1) operaci.

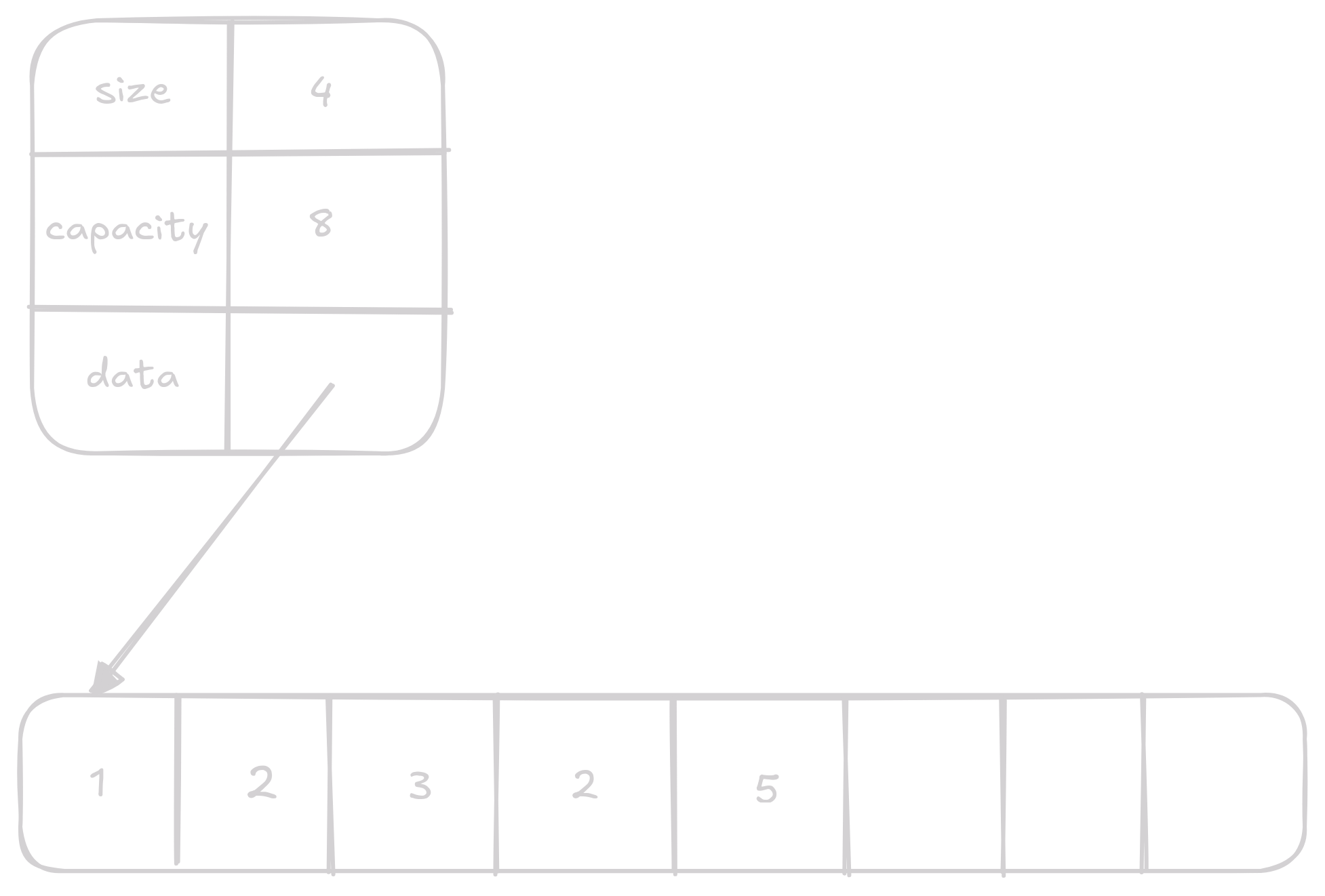
Implementace Vectoru

Stejně jako u linked listu zde je header file a zde implementace.

Struct, kterým budeme vector reprezentovat je tento:

typedef struct {
  int *data;
  size_t size;
  size_t capacity;
} Vector;

Opět budeme potřebovat nadefinovat errory s kterými budeme pracovat:

typedef enum {
  VECTOR_OK,
  VECTOR_ERROR_OUT_OF_BOUNDS,
  VECTOR_ERROR_MEMORY_ALLOCATION,
  VECTOR_ERROR_NULL_POINTER,
} VectorError;

Dále si zadefinujeme konstantu, která nám bude určovat kolikrát se vector zvětší, když bude potřeba více kapacity

#define GROWTH_FACTOR 2

Funkce budou brát pointer na vector na kterém budeme operovat a vracet budou VectorError

Inicializace

Inicializace nastaví úvodní hodnoty vectoru. Často se dělá i init s kapacitou kde se nastaví úvodní kapacita, pro zjednodušení zde tuto variantu psát nebudu.

VectorError vector_init(IntVector *vec) {
  if (vec == NULL) {
    return VECTOR_ERROR_NULL_POINTER;
  }

  vec->size = 0;
  vec->capacity = 4;
  vec->data = malloc(vec->capacity * sizeof(int));

  return (vec->data != NULL) ? VECTOR_OK : VECTOR_ERROR_MEMORY_ALLOCATION;
}

Resize

Resize je helper funkce, která zvětší kapacitu našeho vectoru. Na tento přesun používáme funkci realloc() která přesune data na jiné místo kde je více kapacity.

static VectorError vector_resize(Vector *vec) {
  size_t new_capacity = vec->capacity * GROWTH_FACTOR;
  // realloc nám přesune data na novou adresu s větší kapacitou
  int *new_data = realloc(vec->data, new_capacity * sizeof(int));
  if (new_data == NULL) {
    return VECTOR_ERROR_MEMORY_ALLOCATION;
  }

  vec->data = new_data;
  vec->capacity = new_capacity;
  return VECTOR_OK;
}

Push

Při push musíme zkontrolovat, zda je stále místo na přidání dalšího prvku, pokud místo není použijeme naši helper funkci na resize.

VectorError vector_push(Vector *vec, int value) {
  if (vec == NULL) {
    return VECTOR_ERROR_NULL_POINTER;
  }

  // pokud není dost místa zvýšíme kapacitu
  if (vec->size >= vec->capacity) {
    VectorError error = vector_resize(vec);
    if (error != VECTOR_OK) {
      return error;
    }
  }

  // value zapíšeme do data[vec->size] a poté k vec->size přičteme 1
  vec->data[vec->size++] = value;
  return VECTOR_OK;
}

Pop

Pop je jedna z nejjednodušších operací. Vyžaduje jen kontrolu, že je prvek, který můžeme odstranit. Poté dáme do int *value popnutou hodnotu.

VectorError vector_pop(Vector *vec, int *value) {
  if (vec == NULL) {
    return VECTOR_ERROR_NULL_POINTER;
  }
  if (vec->size == 0) {
    return VECTOR_ERROR_OUT_OF_BOUNDS;
  }

  if (value != NULL) {
    // Bereme hodnotu z vec->size - 1
    // takto rovnou z vec->size i odečteme 1
    *value = vec->data[--vec->size];
  }
  return VECTOR_OK;
}

Insert

Insert opět nejdříve musí zkontrolovat, zda máme dost místa na přidání nového prvku. Poté od posledního prvku k indexu insertu posune všechny prvky o jeden doprava. Tak, jak je tato funkce napsaná je možné dát insert za poslední prvek vectoru pak se bude funkce chovat jako push.

VectorError vector_insert(Vector *vec, size_t index, int value) {
  if (vec == NULL) {
    return VECTOR_ERROR_NULL_POINTER;
  }
  if (index > vec->size) {
    return VECTOR_ERROR_OUT_OF_BOUNDS;
  }

  // realokace v případě nedostatku místa
  if (vec->size >= vec->capacity) {
    VectorError error = vector_resize(vec);
    if (error != VECTOR_OK) {
      return error;
    }
  }

  for (size_t i = vec->size; i > index; --i) {
    // posunutí prvků o jeden doprava od posledního k indexu
    vec->data[i] = vec->data[i - 1];
  }

  vec->data[index] = value;
  vec->size++;
  return VECTOR_OK;
}

Remove

Remove je o něco jednodušší než insert. Není potřeba kontrolovat, zda je nutnost realokace a jediné co se dělá je, že posouváme prvky o jeden doleva.

VectorError vector_remove(Vector *vec, size_t index) {
  if (vec == NULL) {
    return VECTOR_ERROR_NULL_POINTER;
  }
  if (index >= vec->size) {
    return VECTOR_ERROR_OUT_OF_BOUNDS;
  }

  for (size_t i = index; i < vec->size - 1; ++i) {
    // od indexu nastavíme každý prvek na hodnotu dalšího prvku
    vec->data[i] = vec->data[i + 1];
  }

  vec->size--;
  return VECTOR_OK;
}

N-tý prvek

Získání n-tého prvku je převážně jen kontrola, že všechny argumenty, které uživatel dal jsou správně. Poté do pointeru zapíšeme data z n-té pozice. (všimněte si, že používáme const IntVector *vec protože data na které pointer ukazuje, jakkoliv neměníme)

VectorError vector_get(const Vector *vec, size_t index, int *value) {
  if (vec == NULL) {
    return VECTOR_ERROR_NULL_POINTER;
  }
  if (value == NULL) {
    return VECTOR_ERROR_NULL_POINTER;
  }
  if (index >= vec->size) {
    return VECTOR_ERROR_OUT_OF_BOUNDS;
  }

  *value = vec->data[index];
  return VECTOR_OK;
}

Nastavení N-tého prvku

Nastavení n-tého prvku je podobné jako přístup na n-tý prvek jediný rozdíl je, že data z n-té pozice nezískáváme ale zapisujeme do ní.

VectorError vector_set(Vector *vec, size_t index, int value) {
  if (vec == NULL) {
    return VECTOR_ERROR_NULL_POINTER;
  }
  if (index >= vec->size) {
    return VECTOR_ERROR_OUT_OF_BOUNDS;
  }

  vec->data[index] = value;
  return VECTOR_OK;
}

Free

U vectoru musíme uvolnit data a vynulovat zbylé hodnoty. Nic dalšího není potřeba.

void vector_free(Vector *vec) {
  if (vec != NULL) {
    free(vec->data);
    vec->data = NULL;
    vec->size = 0;
    vec->capacity = 0;
  }
}

Hash Table

Hash table někdy taky hashmap už je o něco zajímavější datová struktura. Hash table mapuje unikátní klíče na hodnoty, Výhoda poté je, že dokáže hodnotu podle klíče velmi rychle nalézt. Hash table je společně s vektorem jedna z nejčastěji používaných datových struktur v dynamickém programování.

Reprezerntace

V úplném základu je hash table array pointerů na linked listy. Což znamená že potřebujeme dvě datové struktury jedna, co drží náš array a jedna, která reprezenutuje naše nodes v linked listu. Jedná se o singely linked list, protože ho nidky nebudeme potřebovat traverzovat dozadu (toto je jeden z případů kdy je singly linked list doopravdy vhodný).

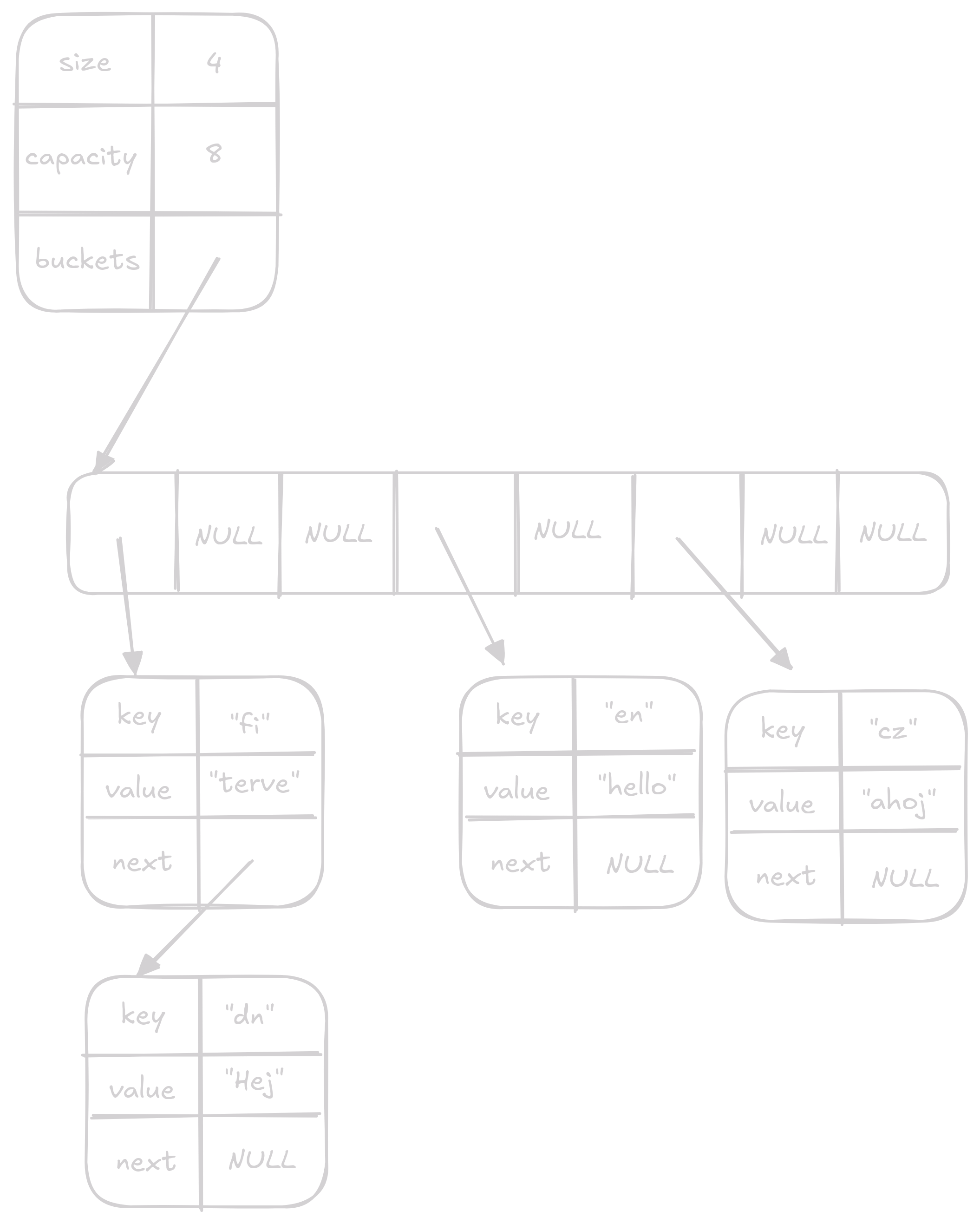
V paměti potom hash table vypadá takto:

// node v linked listu
typedef struct HashTableEntry {
  char *key;
  int value;
  struct HashTableEntry *next;
} HashTableEntry;

// struck hash table
typedef struct {
  HashTableEntry **buckets;
  size_t capacity;
  size_t size;
} HashTable;

Toto je specificky hashtable, který mapuje stringy na čísla. Hashtable ale může mapovat i jiné typy ale poté se musí některé části upravit.

Ok to je pěkný ale, jak to funguje?

Tohle je asi otázka, co máte na mysli potom, co jste viděli monstrozitu výše. Teď projdu krok po kroku, jak jsme se vlastně k této datové struktuře dostali.

Cíl

Naším cílem je vytvořit datovou strukturu kde můžeme jako index pro vyhledávání používat cokoliv, nejen čísla jako je tomu v array/dynamic array.

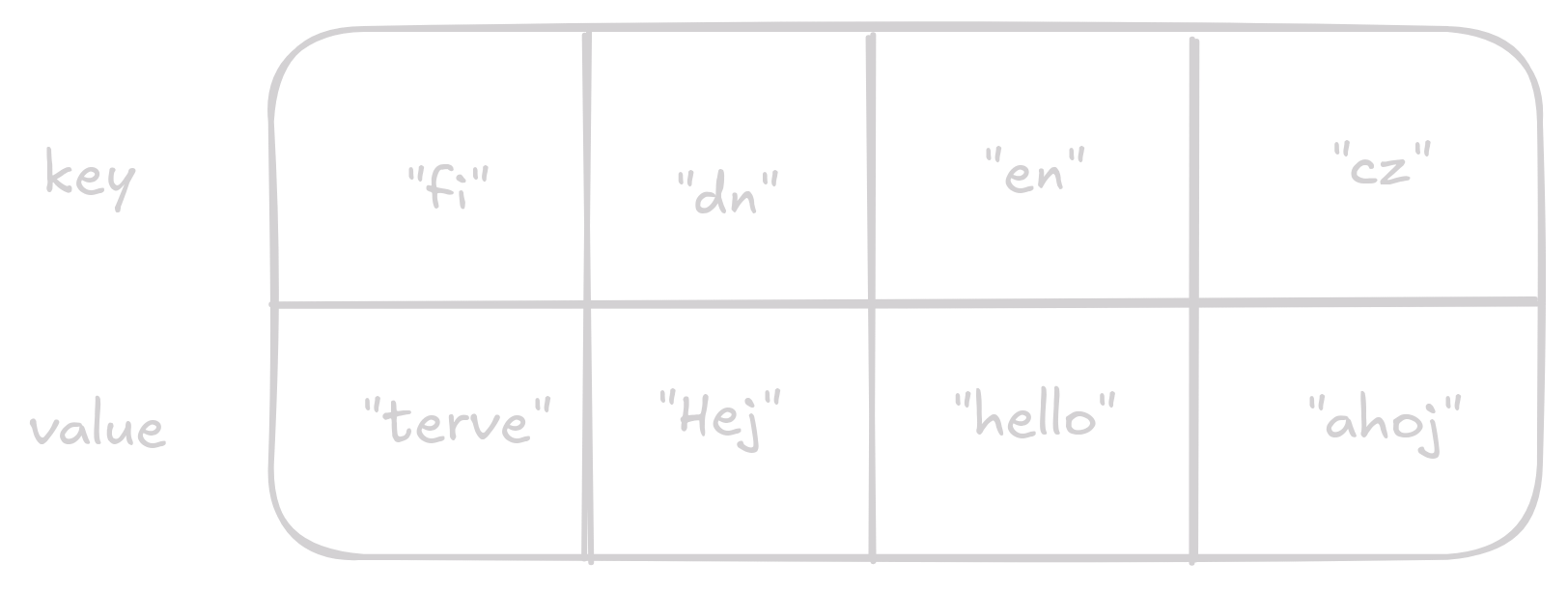
Toho bychom mohly dosáhnout tím, že budeme mít array a klíč převedeme na číslo, které bude indexem v našem array.

Hashing

Pro konverzi klíče na číslo, kterým se pak do array indexujeme využíváme hashing. Jde o proces při, kterém změníme nějáká data na číslo o konstantní velikosti (32 bitů, 64 bitů...). Na hashing standartě používáme hash funkci, po naší hash funkci si přejeme, aby nám vracelo, co nejvíc rozdílná, aby nám vznikalo minimum stejných hashů. Když dva různé klíče mají ten samý hash říkáme tomu hash kolize a zpomaluje to náš hash table. Více o tomto za chvíli.

Pro různá data jsou vhodné různé hash funkce. My budeme implementovat hash table, co má jako klíč string proto budeme používat hash funkci, co je vhodná pro stringy.

Buckets

Teď když máme z našeho klíče číslo musíme ho použít. Náš hash table začne s array o nějáké délce capacity pro náš příklad řekněme 8. Řekněme, že chceme vložit hodnotu "terve" s klíčem "fi". Hash funkce nám vrátí hash 16, takový index nemáme, abychom hash dostali do hodnot validních indexů vymodulujeme ho délkou naší array, to nám dá výsledek 0 (pozn.: hodnoty z hashfunkce jsou vymyšlené pro jednoduchost). Dobrá vložíme hodnotu na index 0 teď by náš array měl vypadato takto.

Teď chceme vložit hodnotu "Hej" s klíčem "dn". Hash funkce nám vrátí hash 24 po vymodulování dostaneme index 0. Yayx nastala kolize, kdybychom teď vložily "Hej" na index 0 přepsali bychom hodnotu "terve" která už tam byla. Tady přijdou na řadu tzv. buckets. Namísto toho abychom na index ukládali jednu hodnotu budeme tam ukládat key value páry v linked listu. Všechny hodnoty v array budou ze začátku NULL pointer, když na nějáký index budeme chtít něco dát dáme to na začátek linked listu na daném indexu.

Tady je, jak by vypadali výše uvedené operace na takovémto array:

1. List plný null pointerů

2. Na index 0 přidáme key value pair "fi", "Terve"

3. Na začátek linked listu na indexu 0 přidáme key value pair "dn", "Hej"

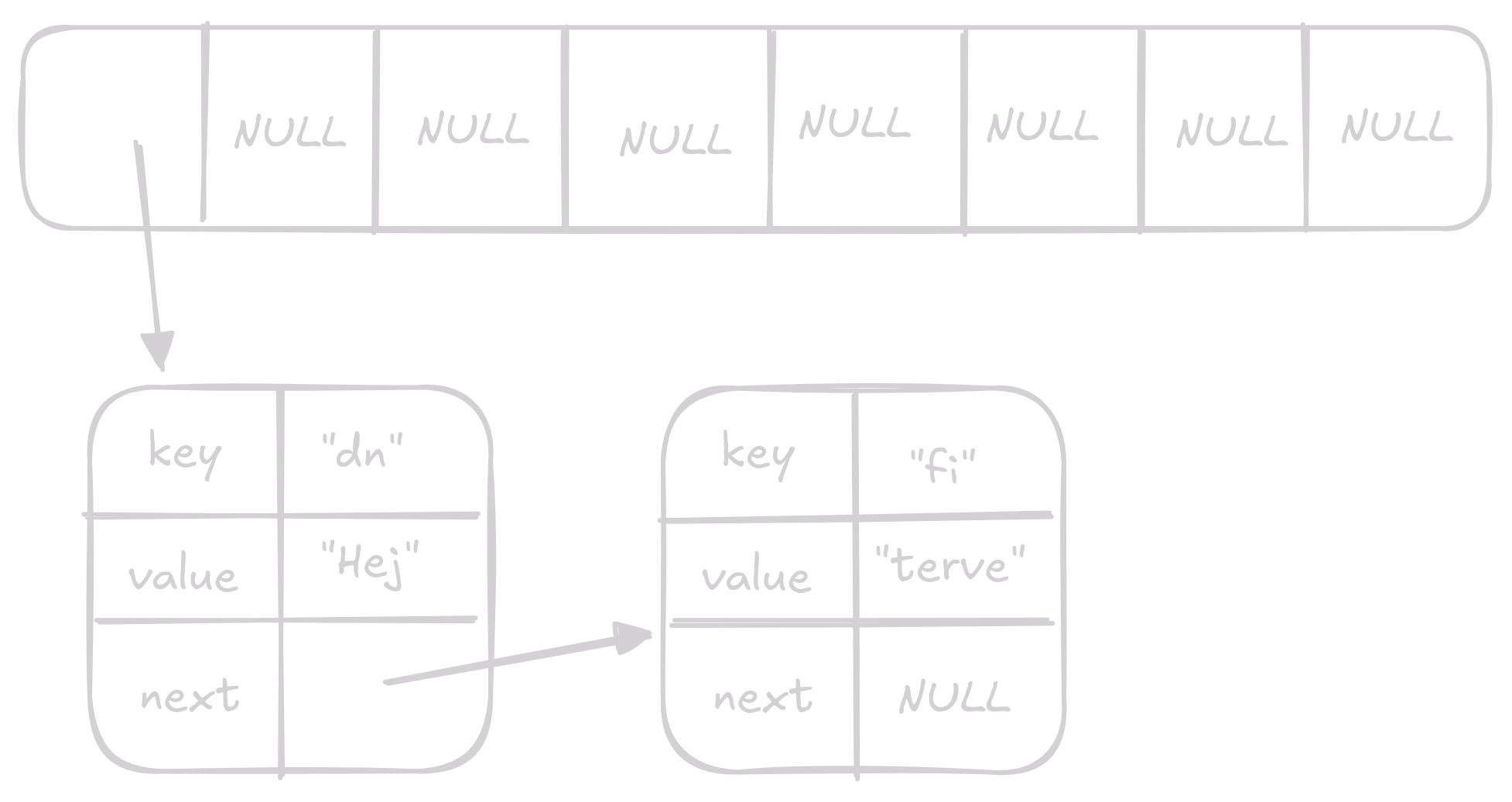
Kolize

Pokud je array na kterém je náš hashtable postaven�ｿ ktátký budou se nám vytvářet dlouhé řetězy, protože bude velké množství klíčů, které skončí v stejném indexu. Pokud musíme hledat v linked listu čas hledání bude lineární což značně zpomalí rychlost našeho hash table. Abychom tomuto zabránily nastavíme, že když učitá čast hash table je zaplňena zvětšíme velikost hash table. Po zvětšení poté musíme všechny key value páry přehashovat a dát na nové indexy.

Operace na Hash Table

Insert

Insert vloží key value pár do hash table. Nejdříve získáme index, kam pár vložit. Poté projdeme projdeme linked list na daném indexu a zkontrolujeme, jestli tam již není hodnota se stejným klíčem, pokud je hodnotu aktualizujeme, pokud ne dáme pár na začátek linked listu. Průměrně bude přístup O(1) ale v chvílích kdy je potřeba zvětšit velikost bude náročnost O(n)

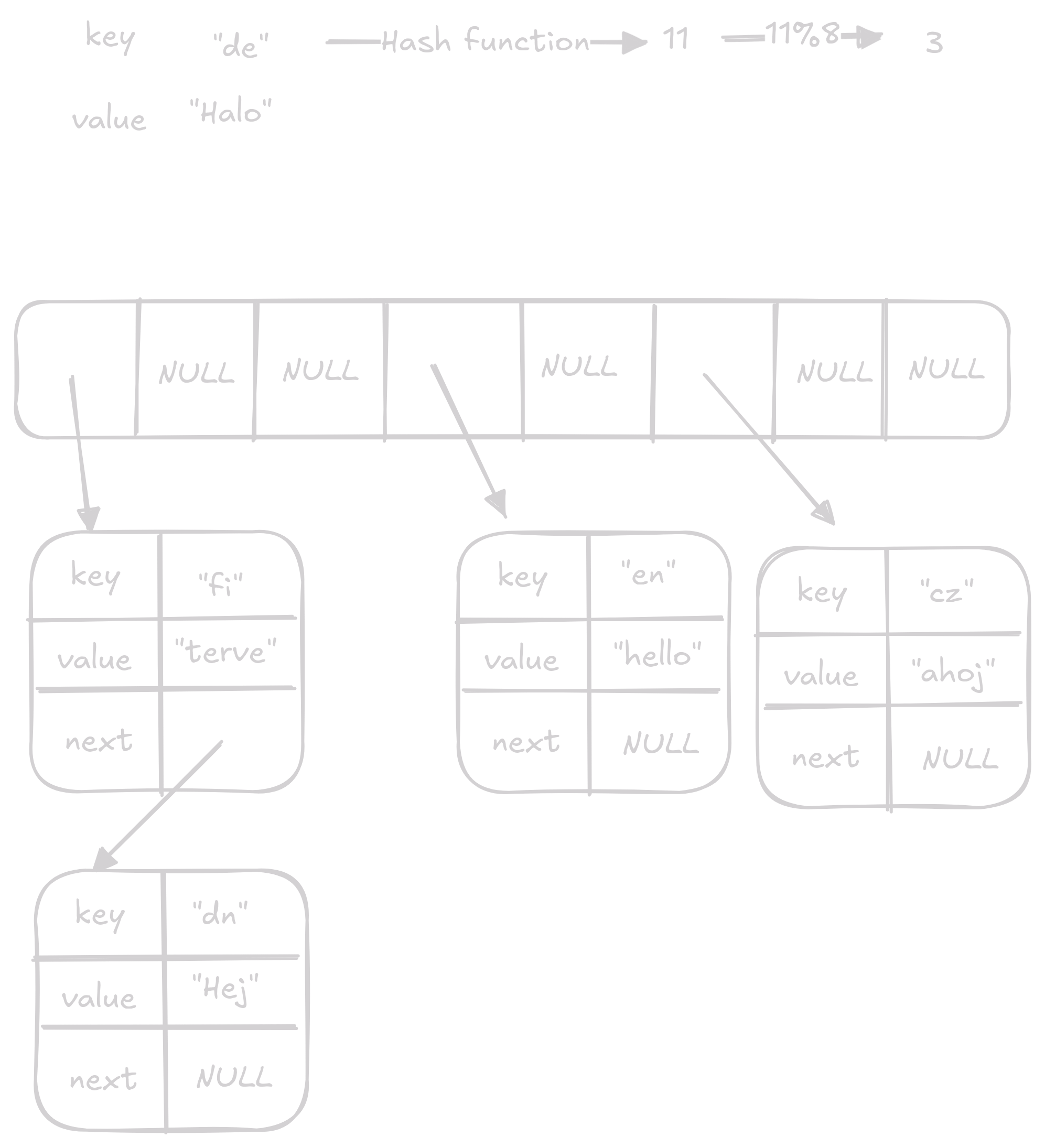
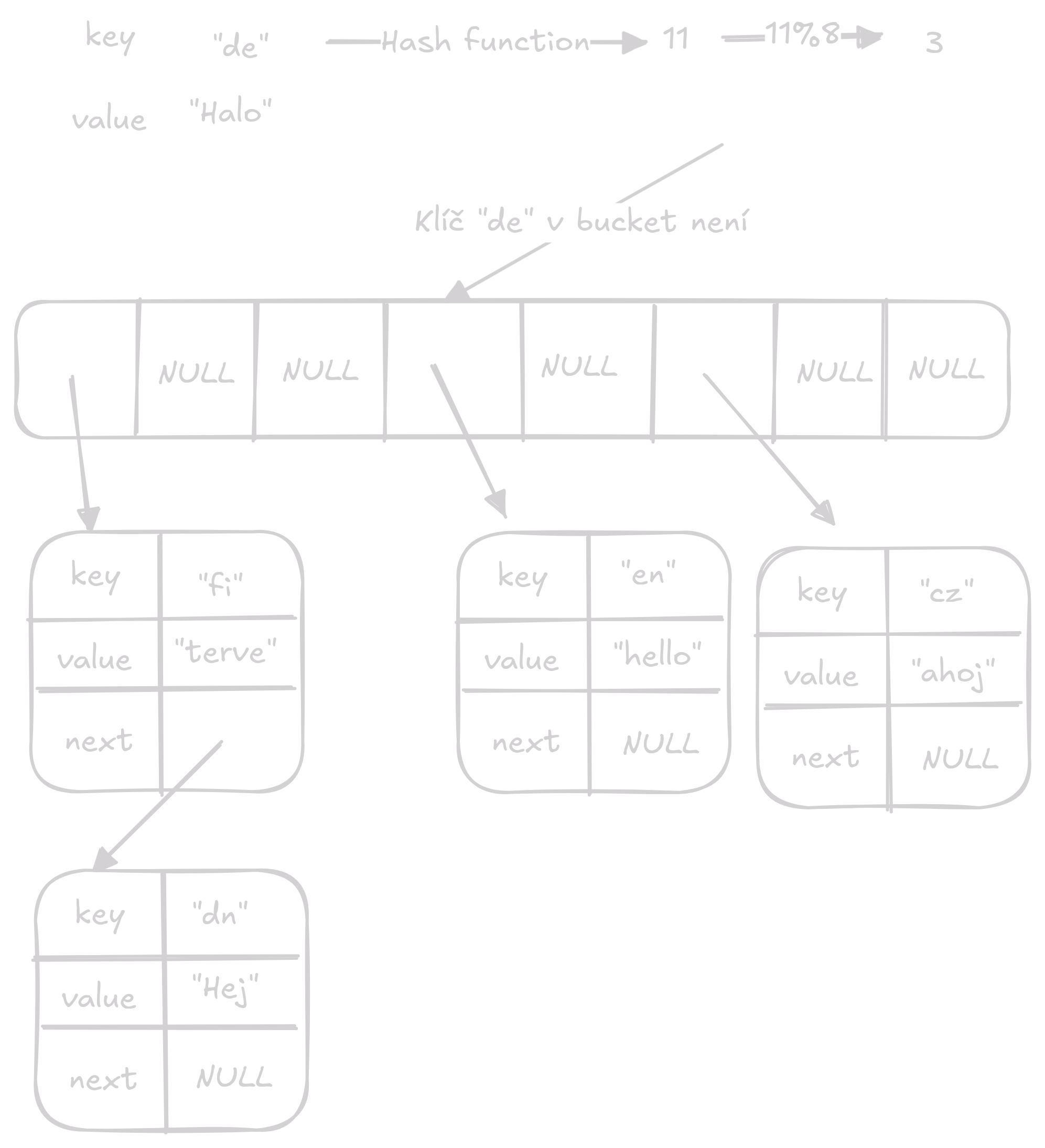
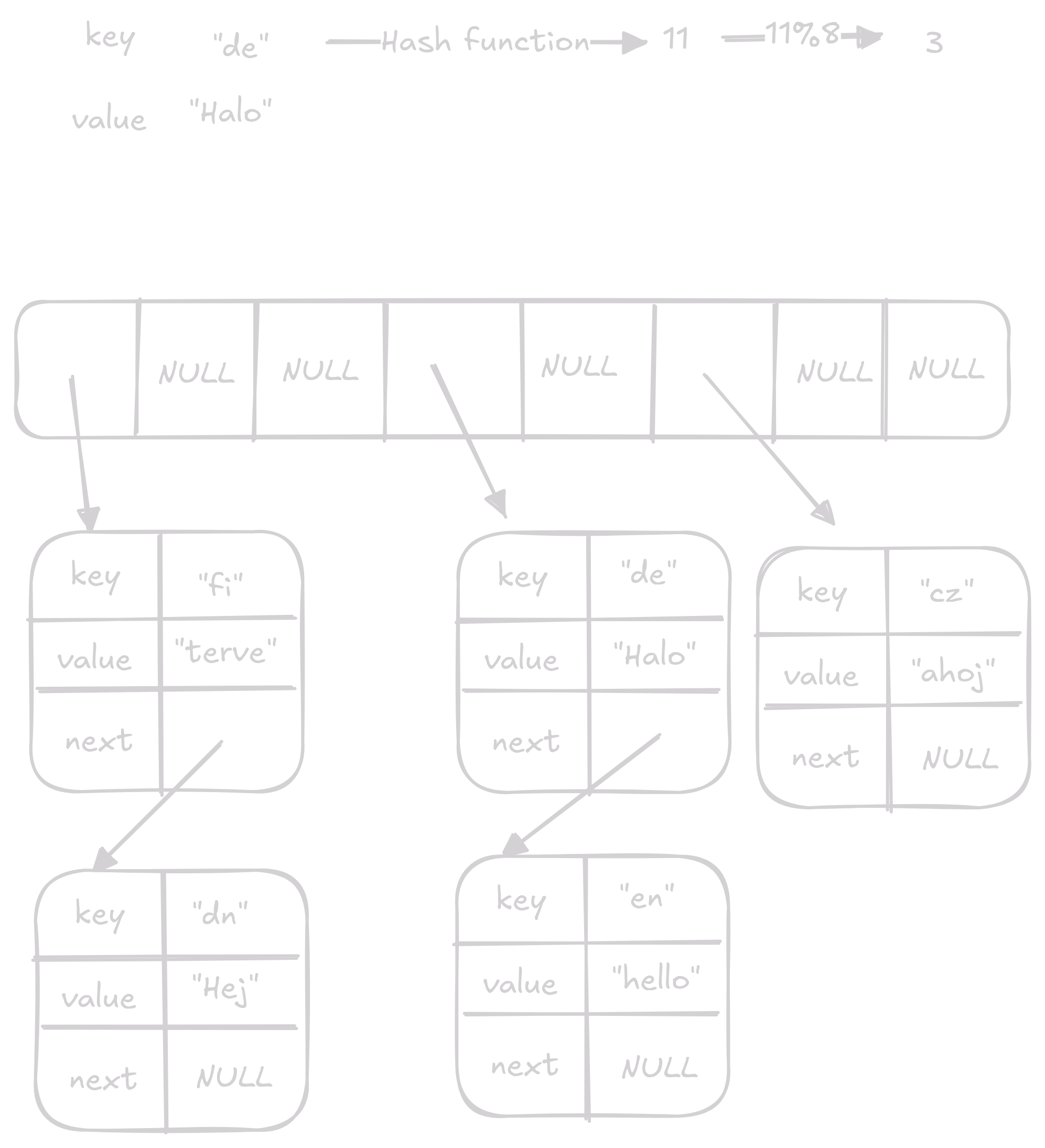
Remove

Remove najde index klíče který chceme odstranit poté projede linked list na daném indexu a z tohoto linked listu odstraní prvek s hledaným klíčem. Jedná se o O(1) operaci ale v nejhorším případě kde jsou všechny páry v jednom linked listu se bude jednat o O(n) operaci.

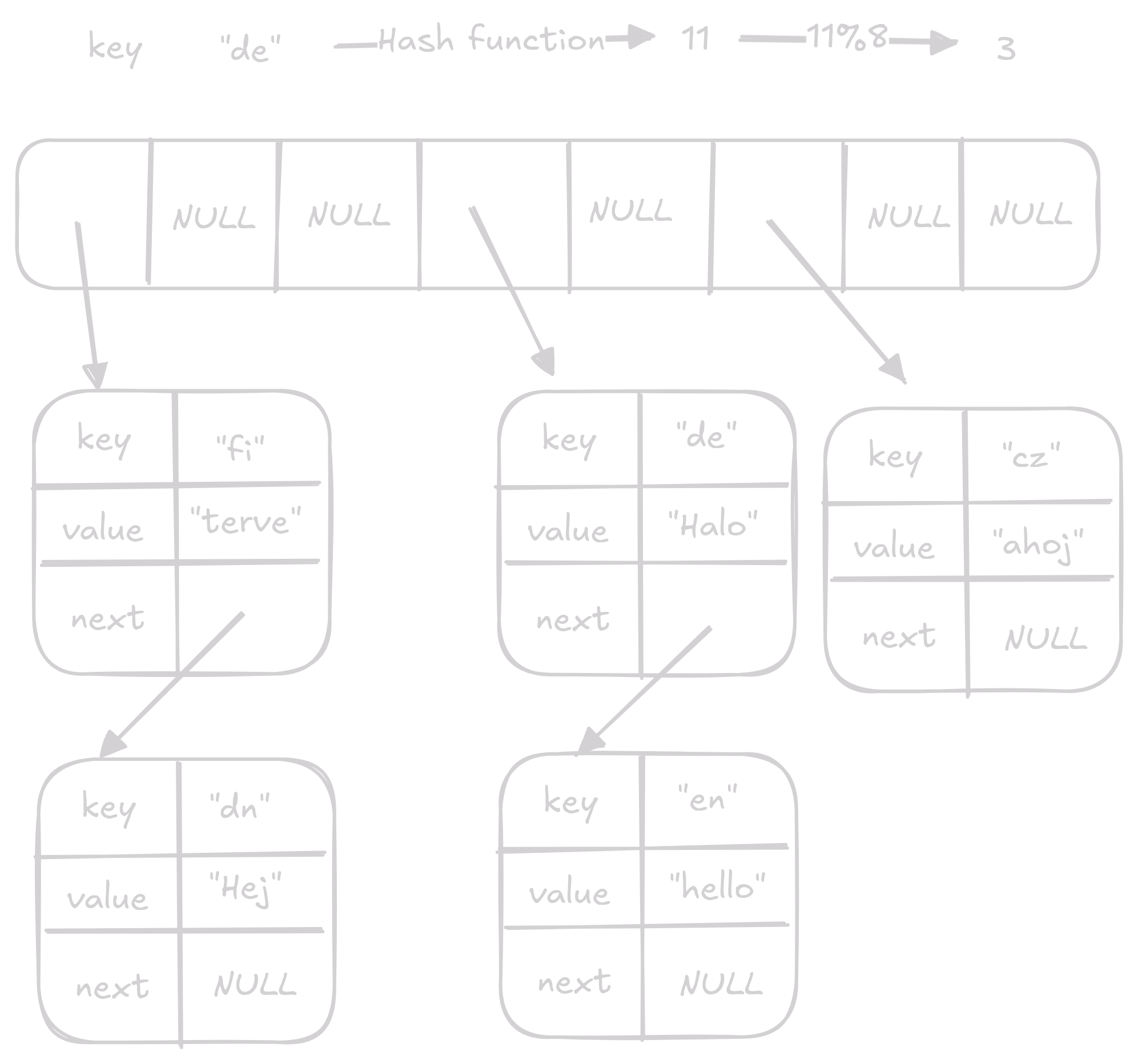
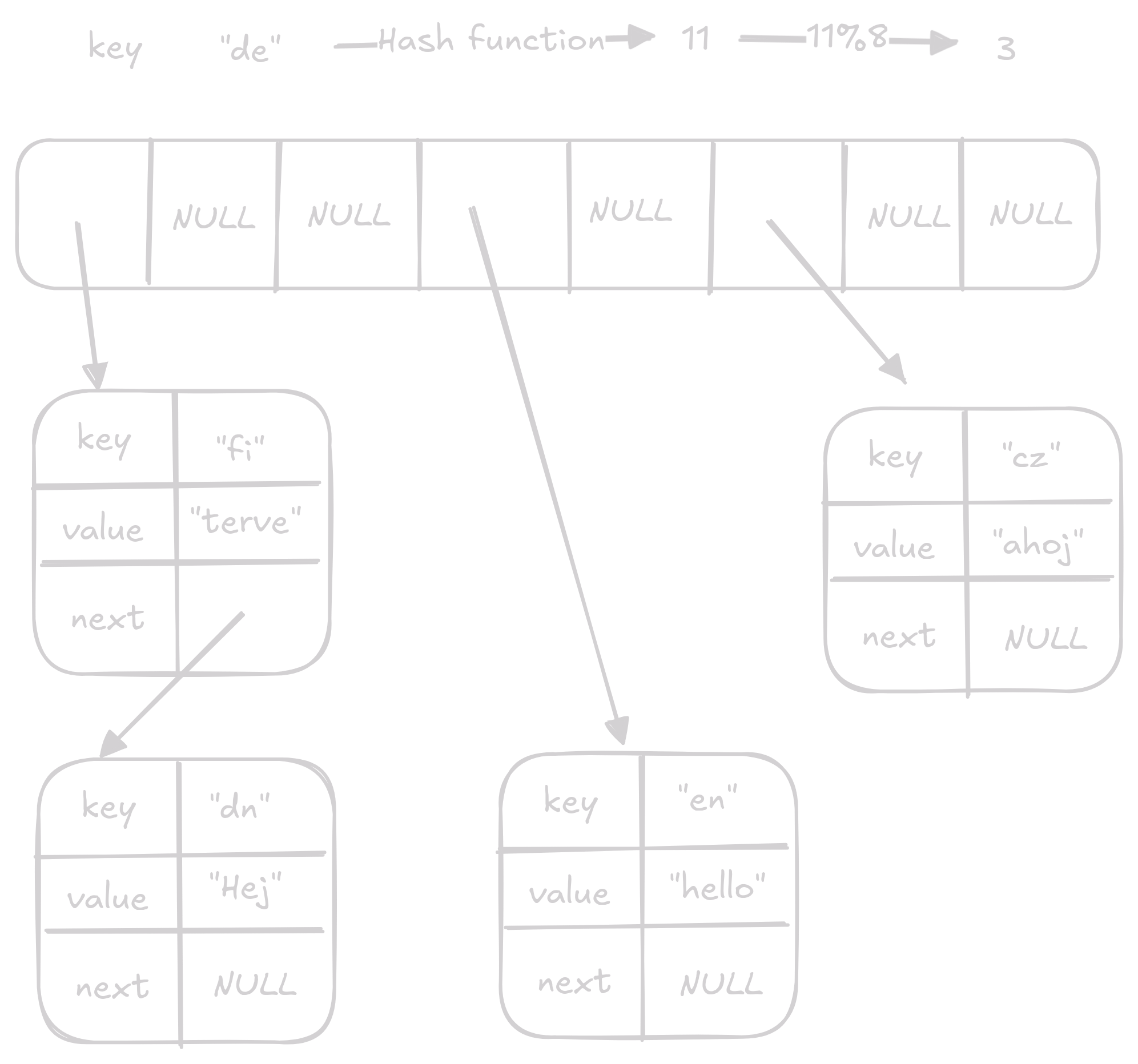
Get

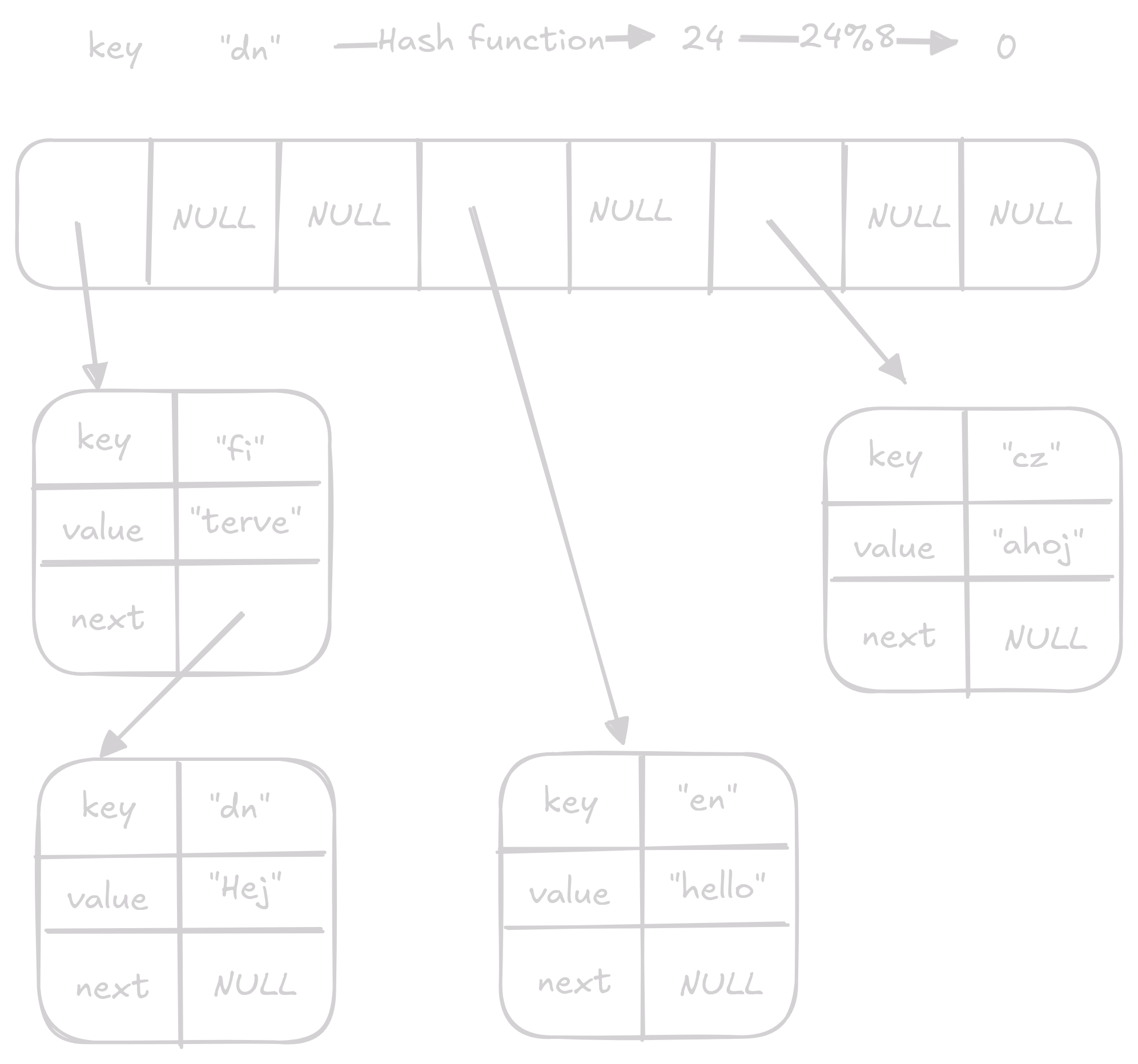
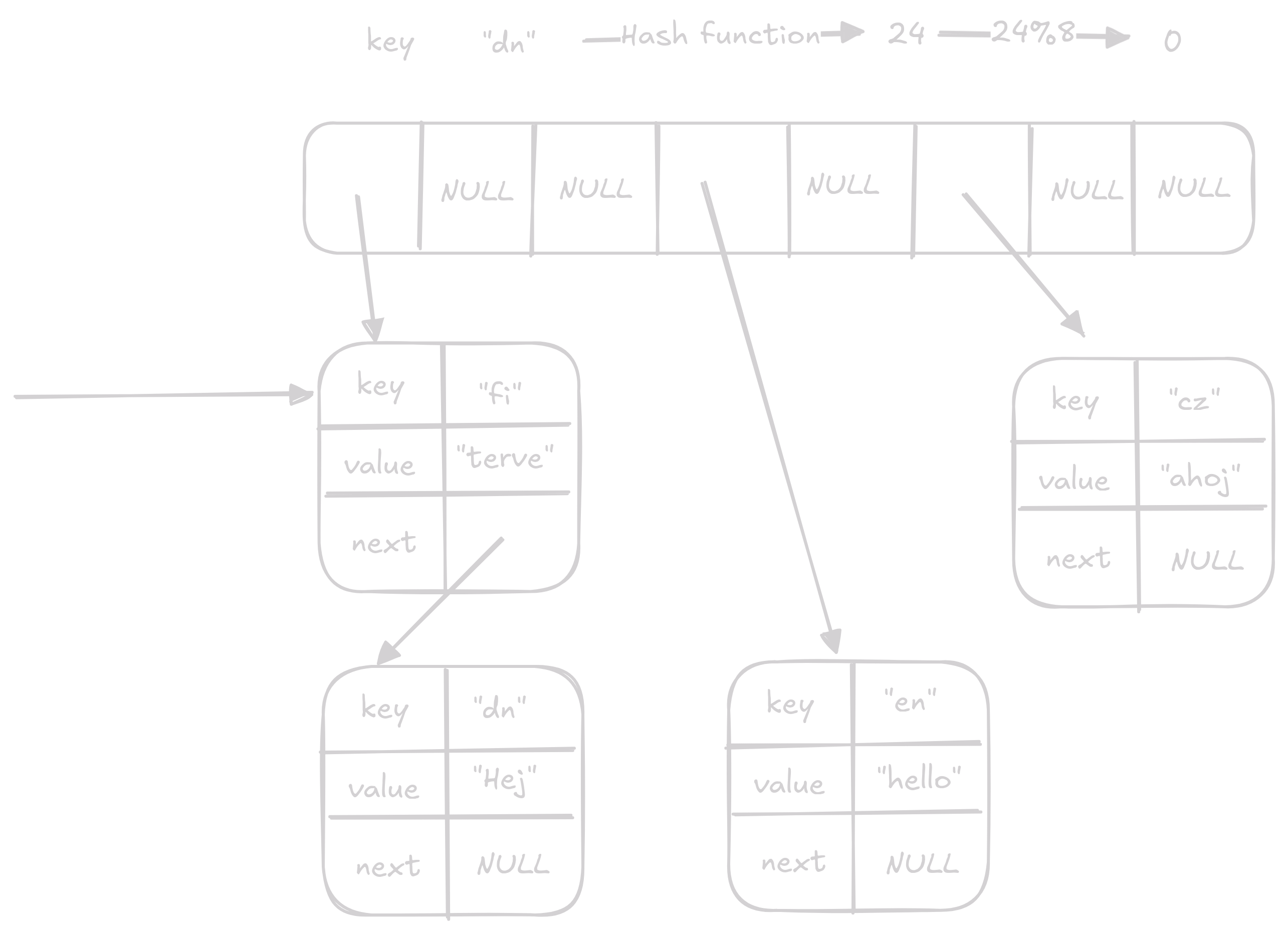
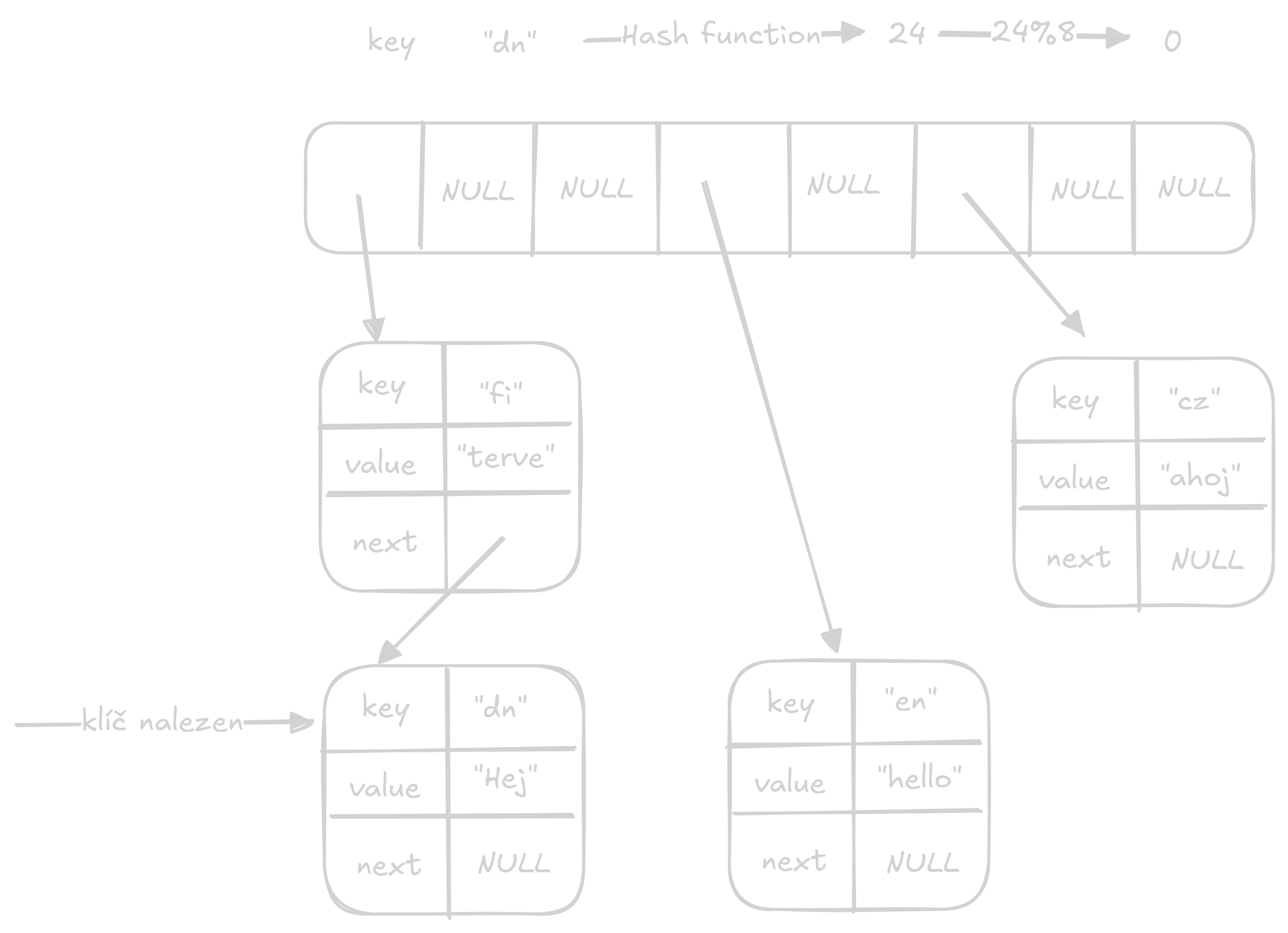
Get získá hodnotu asociovanou s klíčem. Stejně jako u předchozích funkcí získáme index, na kterém by klíč měl být poté projdeme linked list na daném indexu, dokud nenajdeme pár s požadovaným klíčem. Přístup na hodnotu je O(1) operace průměrně a O(n) v nejhorším případě.

Implementace Hash Table

Header file a implementaci můžete najít zde a zde respektive.

Jak jsem již řekl výše budeme psát hash table, který mapuje char * na int. Naše linked list nodes a samotný hast table budou reprezentované těmito strukturami.

typedef struct HashTableEntry {
  char *key;
  int value;
  struct HashTableEntry *next;
} HashTableEntry;

typedef struct {
  HashTableEntry **buckets;
  size_t capacity;
  size_t size;
} HashTable;

A budeme pracovat s těmito errory:

typedef enum {
  HT_OK,
  HT_ERROR_KEY_NOT_FOUND,
  HT_ERROR_MEMORY_ALLOCATION,
  HT_ERROR_NULL_POINTER
} HashTableError;

Dále jsou nějáké konstanty, s kterými budeme pracovat.

#define INITIAL_CAPACITY 16
#define LOAD_FACTOR 0.75f
#define GROWTH_FACTOR 2

Tyto konstanty určují, jaká bude úvodní kapacita hash table, na kolika procentech naplnění se hash table zvětší a kolikrát se zvětší.

Funkce budou brát pointer na HashTable a budou vracet HashTableError

Inicializace

Inicializace nastaví úvodní hodnoty hash table. Občas se dělá funkce, kde můžeme nastavit úvodní parametry pro hash table v tomto případě to pro zjednoduššení nedělám.

HashTableError hashtable_init(HashTable *map) {
  if (!map) {
    return HT_ERROR_NULL_POINTER;
  }

  // calloc nastaví celý prostor na 0 což je ekvivalent jako kdyby všude byly
  // NULL pointery.
  // Toto je důležité abychom později rozpoznali, kde je chain a kde ne
  map->buckets = calloc(INITIAL_CAPACITY, sizeof(HashTableEntry *));
  if (!map->buckets) {
    return HT_ERROR_MEMORY_ALLOCATION;
  }

  map->capacity = INITIAL_CAPACITY;
  map->size = 0;

  return HT_OK;
}

Hash funkce

Protože mapujeme string na int chceme používat hash funkci, která je vhodná pro stringy. Taková funkce už existuje a jmenuje se djb2. Moc se nezamýšlejte nad tím, co dělá nebo jaký význam mají "magické" hodnoty.

static unsigned long hash_function(const char *str) {
  unsigned long hash = 5381;
  int c;

  while ((c = (unsigned char)*str++)) {
    hash = ((hash << 5) + hash) + c;
  }

  return hash;
}

Resize

Resize je interní helper funkce, která zvětší hash table, když je potřeba. Nejdříve vytvoří na heap nový prostor, kam ukládat páry. Poté všechny páry projde, získá nový hash a index a umístí je do nového prostoru.

static HashTableError hashtable_resize(HashTable *map) {
  size_t new_capacity = map->capacity * GROWTH_FACTOR;
  HashTableEntry **new_buckets = calloc(new_capacity, sizeof(HashTableEntry *));
  if (!new_buckets) {
    return HT_ERROR_MEMORY_ALLOCATION;
  }

  // projedem všechny buckets
  for (size_t i = 0; i < map->capacity; i++) {
    HashTableEntry *entry = map->buckets[i];
    // projdeme všechny hodnoty v linked listu získáme nový hash a umístíme do
    // new_buckets
    while (entry) {
      HashTableEntry *next_entry = entry->next;
      unsigned long hash = hash_function(entry->key);
      size_t index = hash % new_capacity;

      entry->next = new_buckets[index];
      new_buckets[index] = entry;

      entry = next_entry;
    }
  }

  free(map->buckets);
  map->buckets = new_buckets;
  map->capacity = new_capacity;

  return HT_OK;
}

Insert

Insert nejdříve získá hash a index kam by měl být pár umístěn. Poté projde linked list na daném indexu a zkontroluje, zda v něm není pár se stejným klíčem, pokud ano hodnotu nahradí. Pokud klíč v linked listu pár je dán na začátek linked listu.

HashTableError hashtable_insert(HashTable *map, const char *key, int value) {
  if (!map || !key) {
    return HT_ERROR_NULL_POINTER;
  }

  unsigned long hash = hash_function(key);
  size_t index = hash % map->capacity;

  HashTableEntry *entry = map->buckets[index];
  // Zde procházíme linked list
  while (entry) {
    // Pokud se klíč rovná klíči momentální prvku aktualizujeme hodnotu a z
    // funkce vrátíme
    if (strcmp(entry->key, key) == 0) {
      entry->value = value;
      return HT_OK;
    }
    entry = entry->next;
  }

  // zde vytvoříme nové entry pomocí helper funkce.
  HashTableEntry *new_entry = hashtable_entry_create(key, value);
  if (!new_entry) {
    return HT_ERROR_MEMORY_ALLOCATION;
  }

  // nastavíme next nového entry na začátek linked listu
  new_entry->next = map->buckets[index];
  // pointer na nový začátek umístíme zpět do arraye
  map->buckets[index] = new_entry;
  map->size++;

  // Pokud je hash table zaplněná více než LOAD_FACTOR hashtable zvětšíme
  if ((float)map->size / map->capacity > LOAD_FACTOR) {
    return hashtable_resize(map);
  }

  return HT_OK;
}

Pomocná funkce hashmap_entry_create(const char *key, int value) vypadá takto.

static HashTableEntry *hashtable_entry_create(const char *key, int value) {
  HashTableEntry *entry = malloc(sizeof(HashTableEntry));
  if (!entry) {
    return NULL;
  }

  entry->key = strdup(key);
  if (!entry->key) {
    free(entry);
    return NULL;
  }

  entry->value = value;
  entry->next = NULL;
  return entry;
}

Remove

Remove projde linked list na získaném indexu, dokud nenarazí na prvek se shodným klíčem. V chvíli, kdy na prvek narazí odstraní ho z linked listu a paměť uvolní.

HashTableError hashtable_remove(HashTable *map, const char *key) {
  if (!map || !key) {
    return HT_ERROR_NULL_POINTER;
  }

  unsigned long hash = hash_function(key);
  size_t index = hash % map->capacity;

  HashTableEntry *entry = map->buckets[index];
  HashTableEntry *prev = NULL;

  // Loop přes linked list
  while (entry) {
    if (strcmp(entry->key, key) == 0) {
      if (prev) {
        // pokud existuje předchozí prvek nastavíme jeho next na next prvku
        // který chceme odstranit.
        prev->next = entry->next;
      } else {
        // pokud je prvek první v svém bucketu umístíme na index jeho next
        map->buckets[index] = entry->next;
      }
      // uvolníme paměť.
      free(entry->key);
      free(entry);
      map->size--;
      return HT_OK;
    }
    prev = entry;
    entry = entry->next;
  }

  // Pokud jsme prošli celý list a prvek jsme nenašli vrátíme error, že klíč v
  // hash table neexistuje.
  return HT_ERROR_KEY_NOT_FOUND;
}

Get

Get projde linked list na získaném indexu, dokud nenarazí na prvek se stejným klíčem. Funkce poté uloží hodnotu do pointeru int *value

HashTableError hashtable_get(HashTable *map, const char *key, int *value) {
  if (!map || !key || !value) {
    return HT_ERROR_NULL_POINTER;
  }

  unsigned long hash = hash_function(key);
  size_t index = hash % map->capacity;

  HashTableEntry *entry = map->buckets[index];
  // loop přes prvky linked listu
  while (entry) {
    if (strcmp(entry->key, key) == 0) {
      *value = entry->value;
      return HT_OK;
    }
    entry = entry->next;
  }

  return HT_ERROR_KEY_NOT_FOUND;
}

Free

Free nejdříve uvolní paměť všech linked listů, a nakonec samotný array buckets.

void hashtable_free(HashTable *map) {
  if (!map) {
    return;
  }

  // projití všech bucketů
  for (size_t i = 0; i < map->capacity; i++) {
    HashTableEntry *entry = map->buckets[i];
    // projití všech prvků linked listů
    while (entry) {
      HashTableEntry *temp = entry;
      entry = entry->next;
      free(temp->key);
      free(temp);
    }
  }
  map->size = 0;
  map->capacity = 0;

  // uvolnění samotné arraye
  free(map->buckets);
}